X
Код презентации скопируйте его
Август Фердинанд Мёбиус
Скачать эту презентацию
Презентация на тему Август Фердинанд Мёбиус
Скачать эту презентациюCлайд 1
Август Фердинанд Мёбиус
Cлайд 2
Родился в Шульпфорте 17.11.1790. Учился в Лепццигском университете (1809 – 1813). Ученик "короля математиков" К. Гаусса в Геттигенском университете (1813-1814). В 1814 изучал математику у И.Ф. Пфаффа в университете в Галле. С 1816 г. начал вести самостоятельные астрономические наблюдения в Плейсенбургской обсерватории. В 1818г. стал ее директором, позже - профессором Лейпцигского университета. Умер 26.09.1868 А жизнь его прошла так...
Cлайд 3
Мёбиус был первоначально астрономом, как Гаусс. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мёбиус стал одним из крупнейших геометров XIX в. Как стал геометром?
Cлайд 4
Cлайд 5
Идея пришла ему в голову, когда служанка неправильно сшила ленту. дальше Oh, I’m sorry!
Cлайд 6
В 1858г. в возрасте 68 лет Мёбиусу удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей. Мебиус послал в Парижскую академию наук работу, включавшую сведения об этом листе. Семь лет он дожидался рассмотрения своей работы и, не дождавшись, опубликовал ее результаты. Открытие века
Cлайд 7
Если попробовать разрезать ленту пополам, разрезая её посередине по линии, параллельной краю, то вместе двух лент получится одна длинная лента с двумя полуоборотами.
Cлайд 8
2) Если разрезать ленту, отпуская от края приблизительно на треть её ширины, то получаются две ленты, одна-более тонкая лента Мебиуса, другая - длинная лента с двумя полуоборотами.
Cлайд 9
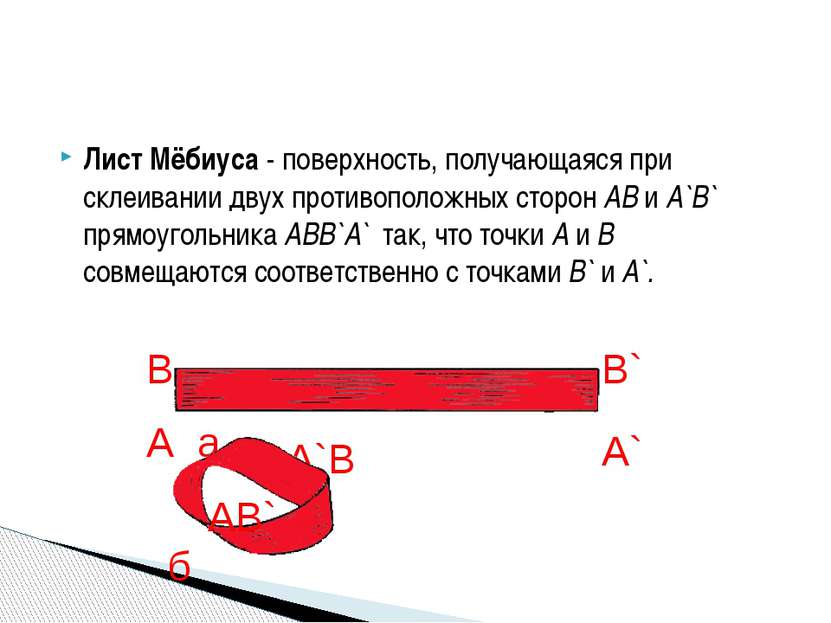
Лист Мёбиуса - поверхность, получающаяся при склеивании двух противоположных сторон AB и А`В` прямоугольника ABB`A` так, что точки А и В совмещаются соответственно с точками B` и A`. А В В` А` а А`В АВ` б
Cлайд 10
Сюрпризы ленты Мебиуса Лента Мёбиуса преподнесет нам не один сюрприз, если вы попытаетесь ее разрезать. Разделим ленту пополам, разрезая её посередине по линии, параллельной краю. Вместо двух лент получится одна длинная лента с двумя полуоборотами (не лента Мёбиуса). дальше
Cлайд 11
Если теперь эту ленту разрезать посередине, то получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами (не лента Мёбиуса). Сюрпризы ленты Мебиуса
Cлайд 12
Именем Мёбиуса назван кратер на обратной стороне Луны.
Cлайд 13
Лист Мёбиуса – желтая страница, Односторонний сказочный маршрут, Летит метелью, песенкой, синицей, Бульварной лентой, склеенный лоскут. Эх, Мёбиус, спасибо за науку! Поверхность одинокой стороны Подобна закольцованному звуку, Вибрацией неоновой струны.
Cлайд 14
У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. ВВЕДЕНИЕ В 1967 году в Бразилии состоялся международный математический конгресс.
Cлайд 15
Его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса. ВВЕДЕНИЕ И монумент высотой более чем в два метра, и крохотная марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета.
Cлайд 16
Лента Мебиуса понравилась не только математикам, но и фокусникам. Более 100 лет лента Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Применение
Cлайд 17
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение. Применение
Cлайд 18
Фотографии образцов конструкций, использующих лист Мёбиуса Силовая конструкция (квадратная), мешалка (большая круглая), винты, испытывающиеся на модели судна (два маленьких круглых) Применение
Cлайд 19
Мотив Ленты Мебиуса встречается в названиях художественных произведений, общественных заведений, логотипах. дальше Международный символ переработки Ресторан «Лента Мебиуса» Инженерно- производственная фирма Мебиус книга футболка серьги компьютерный салон
Cлайд 20
Выводы Лист Мёбиуса находит многочисленные применения в науке, технике и изучении свойств Вселенной. Лента Мебиуса вдохновляет многих художников на создание известных скульптур и картин. Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.
Cлайд 21
Когда родился Август Фердинанд Мёбиус? 1790 1795 1858 Что и когда открыл Мебиус? Лист Мёбиуса кратер на луне 1858 1795 1790 Что это такое? Вопросы на последок!
Cлайд 22
