X
Код презентации скопируйте его
Моделирование. Решение популяционных задач
Скачать эту презентацию
Презентация на тему Моделирование. Решение популяционных задач
Скачать эту презентациюCлайд 1
Карп – мировой рекордсмен, вес 127 кг Пойман на самодельную удочку в 2007г Преподаватель информатики ЖИДКОВ А.В.
Cлайд 2
Популяция и популяционная динамика В биологии: популяция - совокупность особей вида, входящая в состав биогеоценоза. Популяционная динамика, - исследует изменение численности популяции во времени. Математическое моделирование помогает формализовать знания об объекте, дать описание процесса, предсказать его ход и эффективность, дать рекомендации по управлению этим процессом. Это крайне важно для биологических процессов, промышленного назначения - биотехнологических систем, продуктивность которых определяется ростом популяций живых организмов.
Cлайд 3
Популяционная модель неограниченного роста Модель предложена Т. Мальтусом в 1798 г. в его работе "О росте народонаселения". Где - численность популяции в году n; - численность в году n+1; - коэффициент рождаемости. Томас Роберт Мальтус (1766-1834) английский демограф и экономист. Обнаружил, что численность популяций растет в геометрической прогрессии, а производство продуктов питания линейно (в арифметической прогрессии), из чего сделал вывод, что неизбежно наступит мировой голод.
Cлайд 4
Популяционная модель ограниченного роста Впервые ограниченный рост популяции, описал Ферхюльст (1848) – в логистическом уравнении. Это уравнение в дискретном виде Nn+1=Nn+kNn-qNn2 где Nn+1 численность популяции в году n+1; Nn - численность популяции в году n; k – коэффициент рождаемости; q – коэффициент смертности.
Cлайд 5
Популяционная модель ограниченного роста Уравнение ограниченного роста обладает двумя важными свойствами: при малых х численность х возрастает экспоненциально; при больших х - приближается к определенному пределу К. Величина К называется емкость популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования и многими другими факторами, которые могут быть разными для разных видов. Динамика численности жука Rhizopertha dominica в 10-граммовой порции пшеничных зерен, пополняемых каждую неделю. Динамика численности жука Rhizopertha dominica
Cлайд 6
Проверка возможности прогнозирования популяции интерполированием Используя экспериментальные данные, проверить возможность прогнозирования численности популяции обычными методами интерполяции. Сделать выводы о возможности применения этих методов в задачах о численности популяции.
Cлайд 7
Результаты проверки возможности прогнозирования
Cлайд 8
Вывод: Методы интерполяции с использованием трендов, имеющиеся в MS Excel, не могут быть использованы для прогнозирования поведения модели ограниченного роста популяции.
Cлайд 9
Исследование модели популяции
Cлайд 10
Постановка задачи Имеется заброшенный пруд, который может быть использован для разведения карпа. Карпы питаются за счет ресурсов пруда. Параметры прудового хозяйства определены в рамках математической модели ограниченного роста популяции.
Cлайд 11
Описание математической модели Дано: Nn+1 - численность карпа в году n+1. Nn - численность карпа в году n. k=1 – коэффициент рождаемости. q =0,001 – коэффициент смертности. Тогда: Nn+1=Nn + k·Nn- q·Nn2 Число карпов на начало года Родилось карпов за год погибло карпов за год Число карпов к концу года
Cлайд 12
Математическая модель с учетом ежегодного отлова Дано: Nn+1 - численность карпа в году n+1; Nn - численность карпа в году n; k=1 – коэффициент рождаемости; q =0,001 – коэффициент смертности; U – ежегодный улов, заданный количеством особей Тогда: Nn+1=Nn+k·Nn-q·Nn2-U Число карпов на начало года Родилось карпов за год погибло карпов за год Число карпов к концу года отловлено карпов за год
Cлайд 13
Популяция карпа компьютерная модель в Excel Размещение исходных данных.
Cлайд 14
Цель моделирования Определить емкость популяции. Определить максимальный годовой улов рыбы, после стабилизации популяции на уровне емкости популяции. Определить с какого года возможно отлавливать рыбу в максимальном размере. Определить какое количество элитных мальков карпа надо запустить в пруд, чтобы начать отлов на максимальном уровне уже через год. Определить через сколько лет окупятся затраты на приобретение элитных мальков. (Кредит 20% годовых) Исследовать влияние коэффициента рождаемости на динамику популяции, дать своё обоснование каждому из полученных графиков.
Cлайд 15
Задание Создать отчет о проведенном исследовании в виде презентации. 1.Слайд «Название и автор». 2.Исследование возможности прогнозирования 3. Слайд «Математическая модель». 4. Слайд «Реализация модели в Excel». 5-11. Слайды ответы на вопросы исследования. 12. Слайд «Направление дальнейших исследований».
Cлайд 16
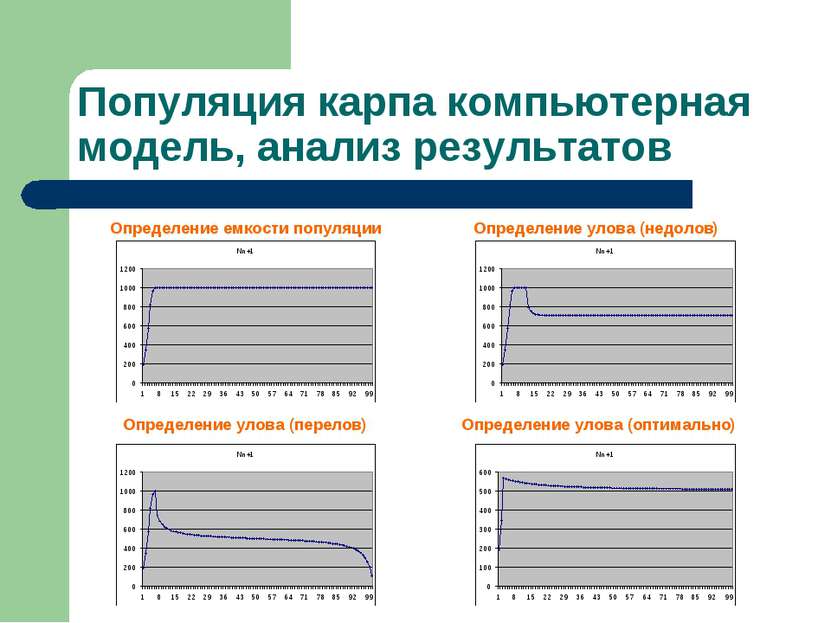
Популяция карпа компьютерная модель, анализ результатов Определение емкости популяции Определение улова (недолов) Определение улова (перелов) Определение улова (оптимально)
Cлайд 17
Исследование влияния коэффициента рождаемости
Cлайд 18
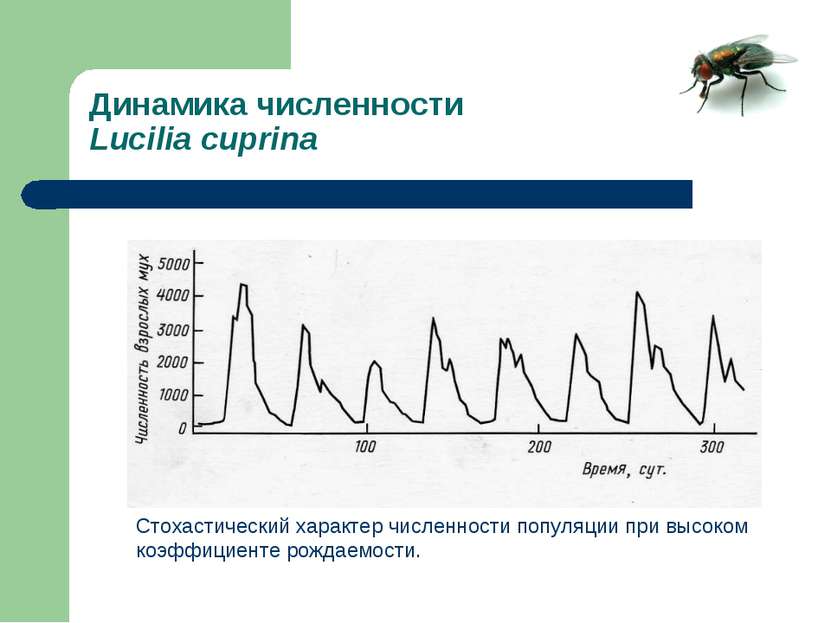
Динамика численности Lucilia cuprina Стохастический характер численности популяции при высоком коэффициенте рождаемости.
Cлайд 19
Список источников информации Задачник по моделированию «Информатика и ИКТ» 9-11 класс, Макарова Н.В., «Питер», 2008 год. Избранные вопросы математического моделирования и численных методов. Учебное пособие. Автор/создатель: Тарасевич Ю.Ю.,Год: 2004. (http://window.edu.ru/library/pdf2txt/936/38936/16634/page6). Г.Ю.Ризниченко Популяционная динамика (http://www.library.biophys.msu.ru/MathMod/PD.HTML). Видео ролик video.raid.ru/pages/video/58845/. Динамика численности Lucilia cuprina http://www.slidefinder.net/l/lect_15_fert_human_pop_growth/32718196/p2. festival.1september.ru/articles/571753/prez.ppt kvlar.3dn.ru/dowl/dinamika_populiacii.ppt http://www.metod-kopilka.ru/page-2-2-9-9.html
Cлайд 20
ЖЕЛАЮ УСПЕХОВ
