X
Код презентации скопируйте его
Свойство скрещивающихся рёбер правильной треугольной пирамиды
Скачать эту презентацию
Презентация на тему Свойство скрещивающихся рёбер правильной треугольной пирамиды
Скачать эту презентациюCлайд 1
Рекомендации к решению №260, №261, С2 ЕГЭ - 2011 Методическая разработка учителя Поляковой Е. А.
Cлайд 2
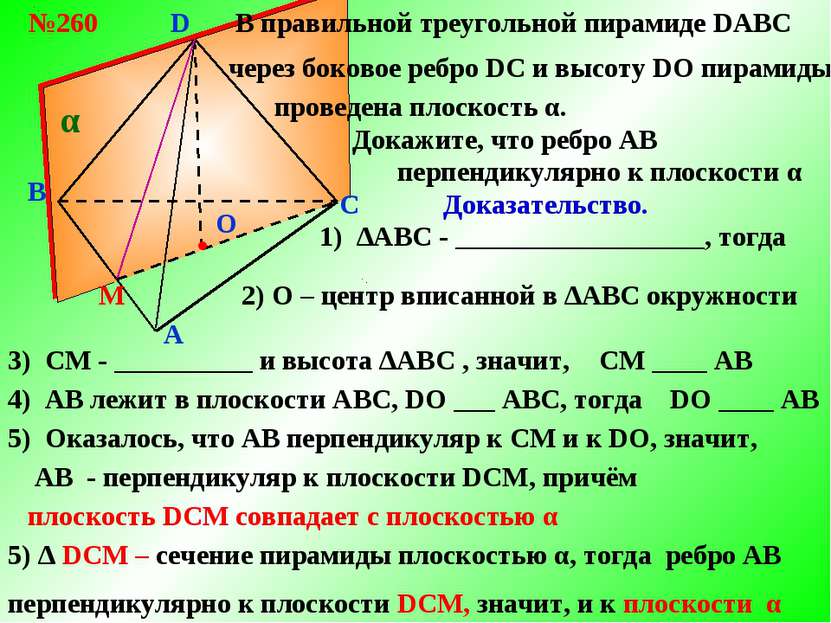
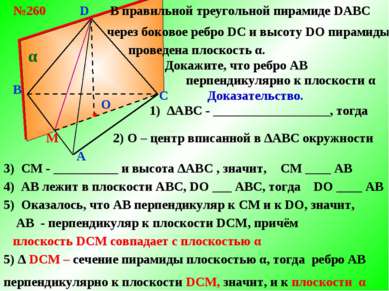B A C D О В правильной треугольной пирамиде DABC №260 через боковое ребро DС и высоту DO пирамиды проведена плоскость α. М Докажите, что ребро АB перпендикулярно к плоскости α α Доказательство. ● 1) ∆АBС - __________________, тогда 2) О – центр вписанной в ∆АBС окружности 3) СМ - __________ и высота ∆АBС , значит, 4) АВ лежит в плоскости АBС, DO ___ АВС, тогда СМ ____ АB DO ____ АB 5) Оказалось, что АВ перпендикуляр к СМ и к DO, значит, АВ - перпендикуляр к плоскости DСM, причём 5) ∆ DСM – сечение пирамиды плоскостью α, тогда ребро АB плоскость DСM совпадает с плоскостью α перпендикулярно к плоскости DСM, значит, и к плоскости α
Cлайд 3
Свойство скрещивающихся рёбер правильной треугольной пирамиды
Cлайд 4
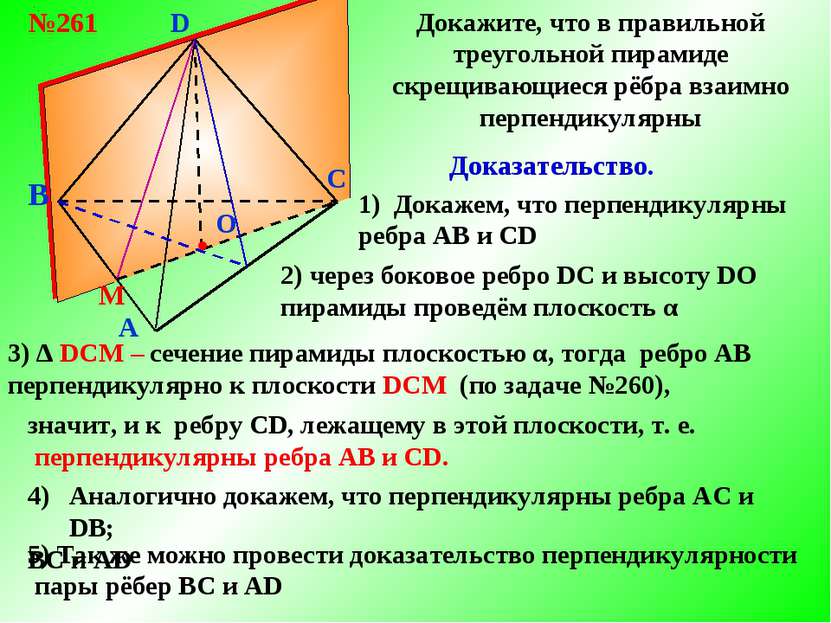
B A C D №261 Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра взаимно перпендикулярны Доказательство. 1) Докажем, что перпендикулярны ребра АВ и CD 2) через боковое ребро DС и высоту DO пирамиды проведём плоскость α О М ● 3) ∆ DСM – сечение пирамиды плоскостью α, тогда ребро АB перпендикулярно к плоскости DСM (по задаче №260), значит, и к ребру CD, лежащему в этой плоскости, т. е. перпендикулярны ребра АВ и CD. Аналогично докажем, что перпендикулярны ребра АС и DВ; ВС и AD 5) Так же можно провести доказательство перпендикулярности пары рёбер ВС и AD
Cлайд 5
Применение свойства скрещивающихся рёбер правильной треугольной пирамиды в задаче С2 ЕГЭ - 2011
Cлайд 6
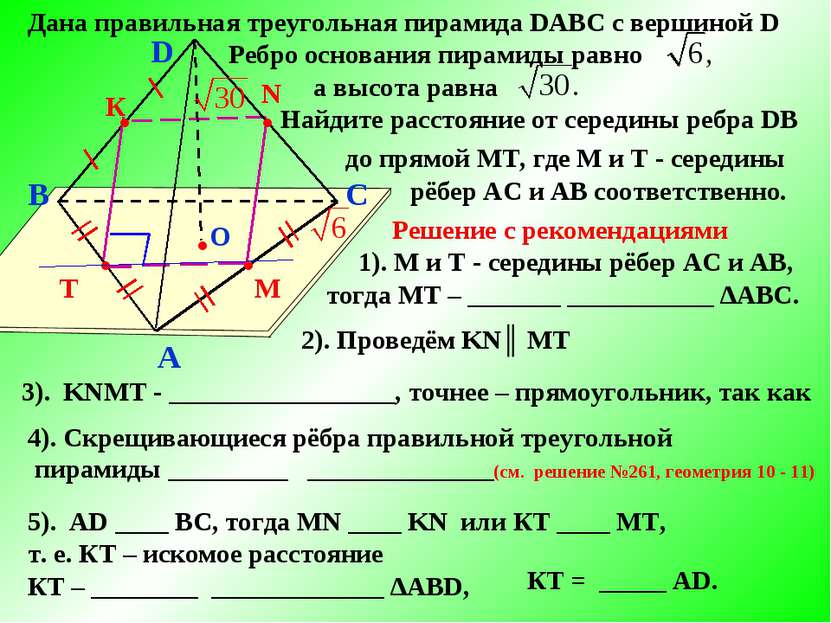
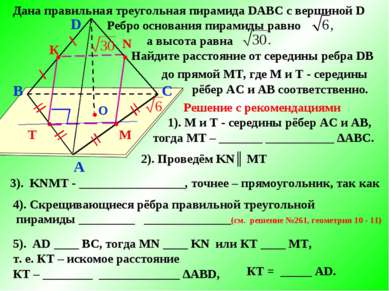B A C D О T ● ● М N ● ● Дана правильная треугольная пирамида DABC с вершиной D Ребро основания пирамиды равно а высота равна Найдите расстояние от середины ребра DB до прямой МТ, где М и Т - середины рёбер АС и АВ соответственно. К Решение с рекомендациями 1). М и Т - середины рёбер АС и АВ, тогда МТ – _______ ___________ ∆АВС. 2). Проведём KN║ МТ 3). KNМТ - _________________, точнее – прямоугольник, так как 4). Скрещивающиеся рёбра правильной треугольной пирамиды _________ ______________(см. решение №261, геометрия 10 - 11) 5). AD ____ ВС, тогда MN ____ KN или КТ ____ МТ, т. е. КТ – искомое расстояние ● КТ – ________ _____________ ∆АВD, КТ = _____ AD.
Cлайд 7
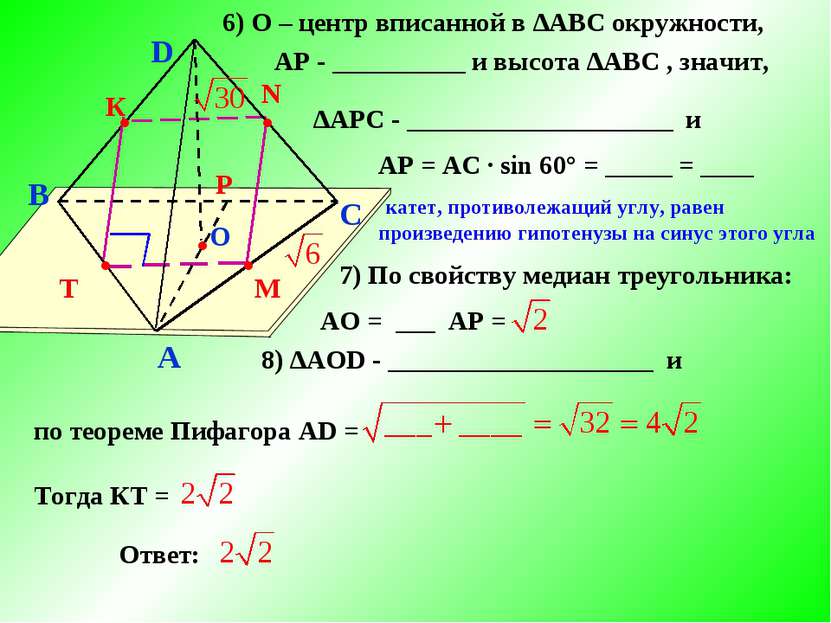
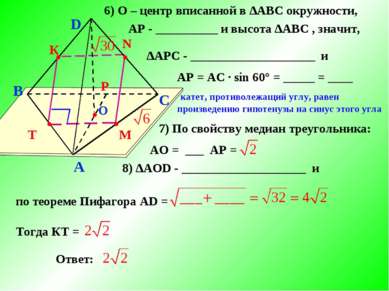B A C D О T ● ● М N ● ● К ● Р 6) О – центр вписанной в ∆АBС окружности, АР - __________ и высота ∆АBС , значит, ∆АPС - ____________________ и АР = АС ∙ sin 60° = _____ = ____ катет, противолежащий углу, равен произведению гипотенузы на синус этого угла 7) По свойству медиан треугольника: АО = ___ АР = 8) ∆АOD - ____________________ и по теореме Пифагора AD = Тогда КТ = Ответ:
