X
Код презентации скопируйте его
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
Скачать эту презентацию
Презентация на тему УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
Скачать эту презентациюCлайд 1
Презентация выполнена учителем математики МОУ «СОШ№6» п.Передового Ставропольского края Богдановской Валентиной Михайловной
Cлайд 2
Четырехугольная призма Повтори формулы: Где a,b,c – длина, ширина и высота параллелепипеда, d- длина диагонали основания, D- диагональ призмы, d- диагональ основания, S- площадь основания, Q- площадь диагонального сечения, Sб- площадь боковой поверхности, β –угол между диагональю параллелепипеда и плоскостью основания
Cлайд 3
Ребро куба равно а. Найдите: Диагональ грани d= a√2 Диагональ куба D= a√3 Периметр основания P= 4a Площадь грани S=a2 Площадь диагонального сечения Q= a2√2 Площадь поверхности куба S= 6a2 Периметр и площадь сечения, проходящего через концы трех ребер, выходящих из одной вершины P= 3a√2 а
Cлайд 4
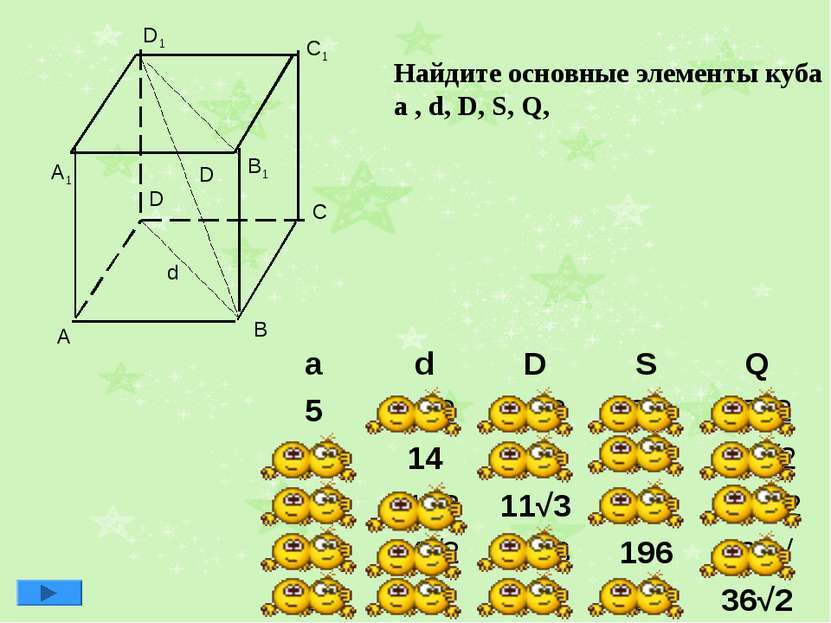
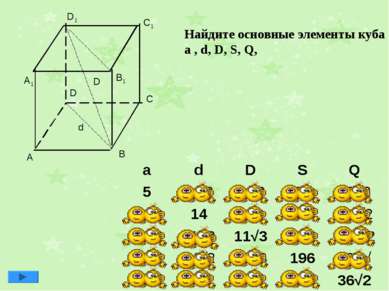Найдите основные элементы куба a , d, D, S, Q, d D a d D S Q 5 5 √2 5 √3 25 25√2 7√2 14 7√6 98 98 √2 11 11√2 11√3 121 121√2 14 14√2 14√3 196 196√ 6 6√2 6√3 36 36√2
Cлайд 5
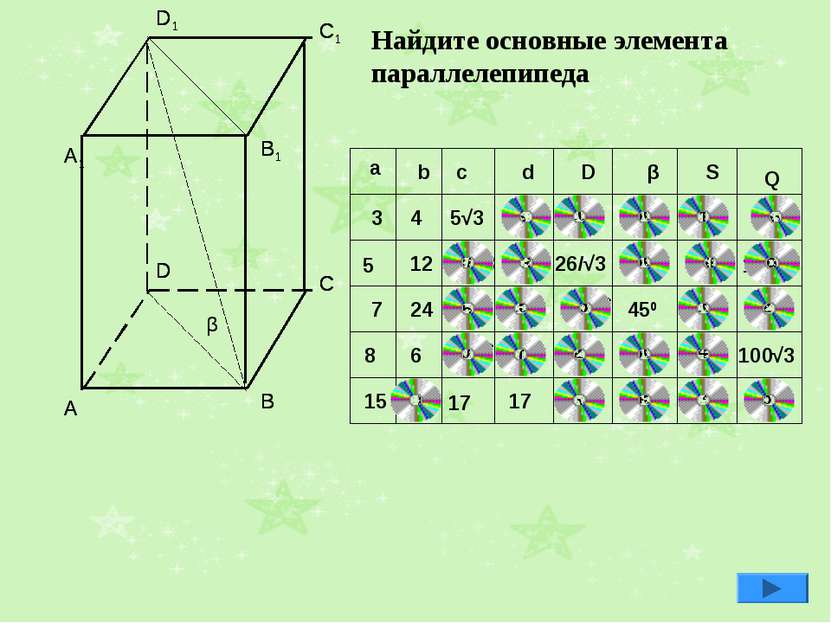
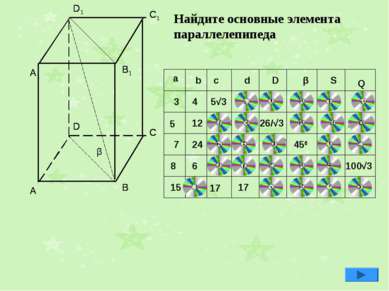β a b c d D β S Q 7 8 15 4 12 24 6 5√3 17 17 26/√3 450 100√3 10 600 12 25√3 3 5 5 13/√3 13 300 300 300 60 60 169√3 25 25 25 25√2 25√2 168 625 10 10√3 20 600 48 8 450 17√2 120 120 289 Найдите основные элемента параллелепипеда
Cлайд 6
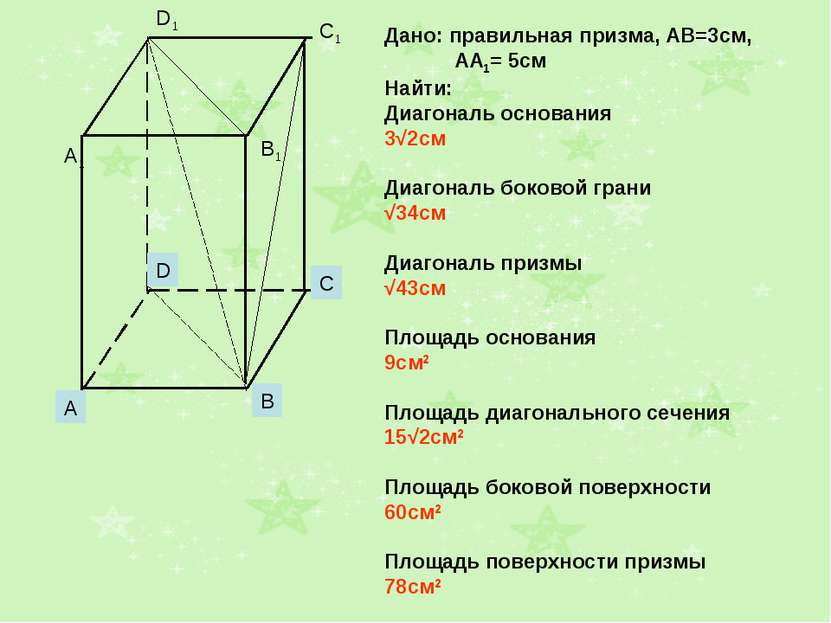
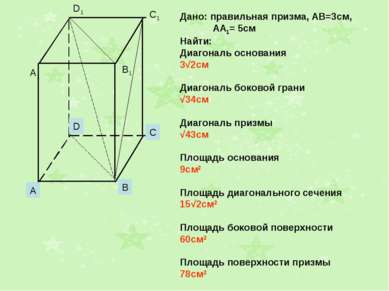Дано: правильная призма, АВ=3см, АА1= 5см Найти: Диагональ основания 3√2см Диагональ боковой грани √34см Диагональ призмы √43см Площадь основания 9см2 Площадь диагонального сечения 15√2см2 Площадь боковой поверхности 60см2 Площадь поверхности призмы 78см2
Cлайд 7
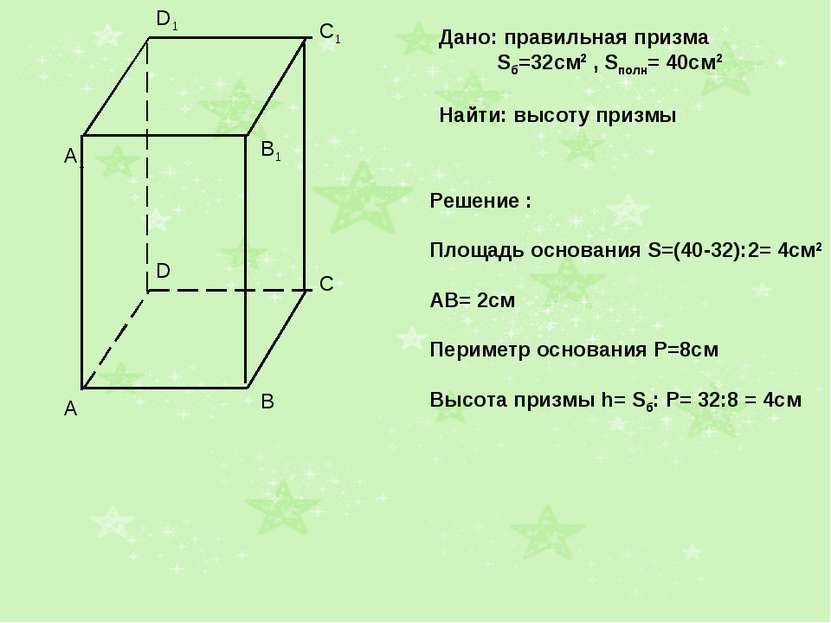
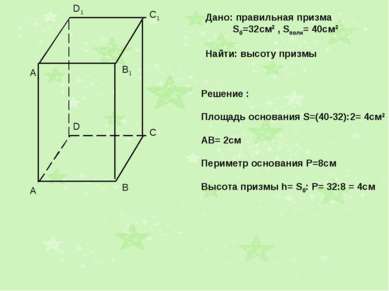Дано: правильная призма Sб=32см2 , Sполн= 40см2 Найти: высоту призмы Решение : Площадь основания S=(40-32):2= 4см2 АВ= 2см Периметр основания Р=8см Высота призмы h= Sб: Р= 32:8 = 4см
Cлайд 8
ТРЕУГОЛЬНАЯ, ШЕСТИУГОЛЬНАЯ И n-УГОЛЬНАЯ ПРИЗМЫ Повтори формулы: Sб= РН Sп= Sб+2s Р = 3а Р = 6а Для правильной треугольной призмы Для произвольной призмы Для правильной шестиугольной призмы
Cлайд 9
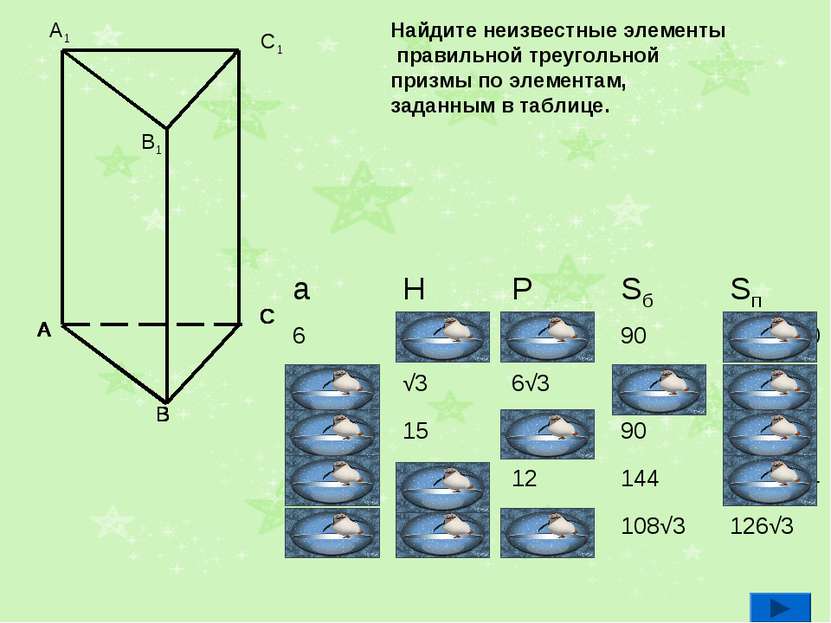
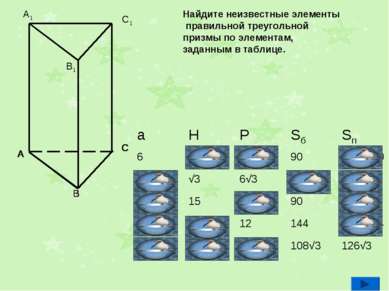Найдите неизвестные элементы правильной треугольной призмы по элементам, заданным в таблице. A B C A A B C A B C A B C A B C A B C A B A
Cлайд 10
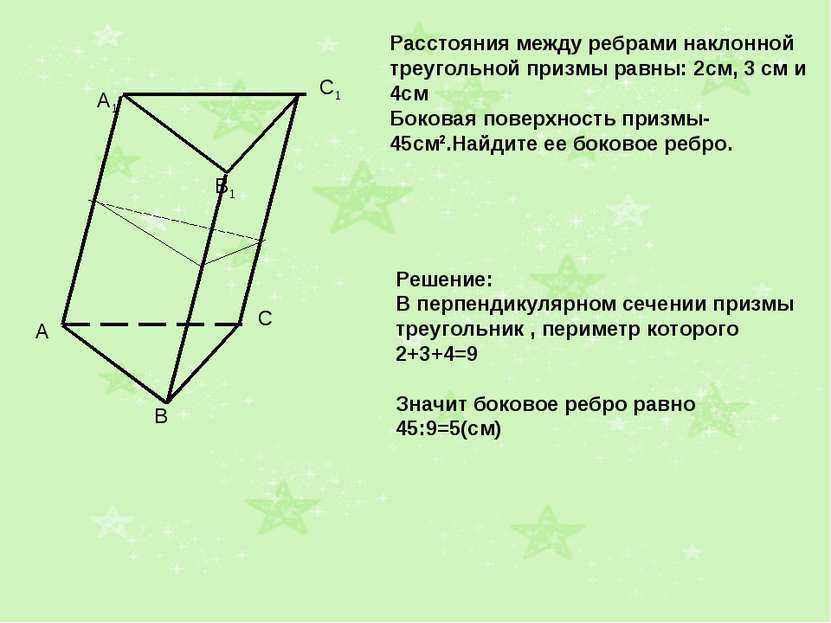
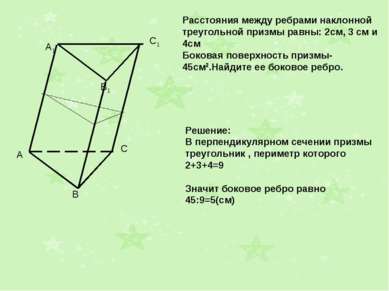A1 B1 C1 Расстояния между ребрами наклонной треугольной призмы равны: 2см, 3 см и 4см Боковая поверхность призмы- 45см2.Найдите ее боковое ребро. Решение: В перпендикулярном сечении призмы треугольник , периметр которого 2+3+4=9 Значит боковое ребро равно 45:9=5(см)
Cлайд 11
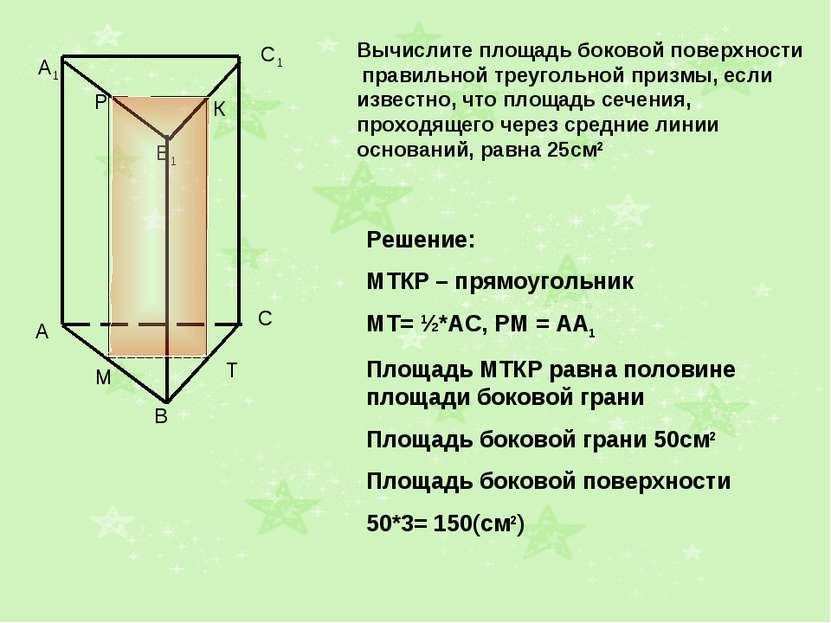
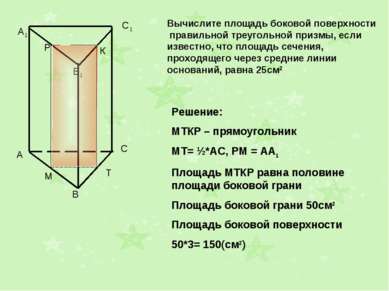A1 B1 C1 Вычислите площадь боковой поверхности правильной треугольной призмы, если известно, что площадь сечения, проходящего через средние линии оснований, равна 25см2 Решение: МТКР – прямоугольник МТ= ½*АС, РМ = АА1 Площадь МТКР равна половине площади боковой грани Площадь боковой грани 50см2 Площадь боковой поверхности 50*3= 150(см2) М Т Р К
Cлайд 12
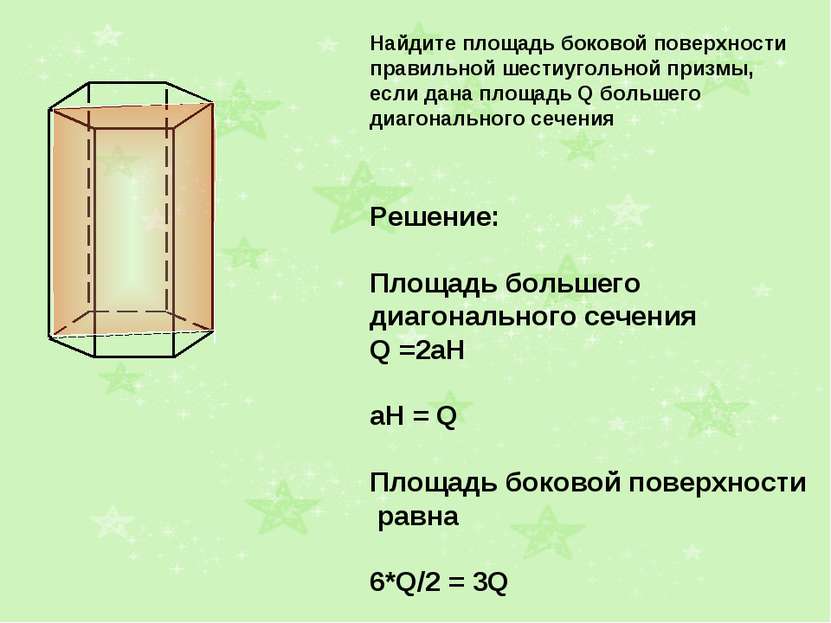
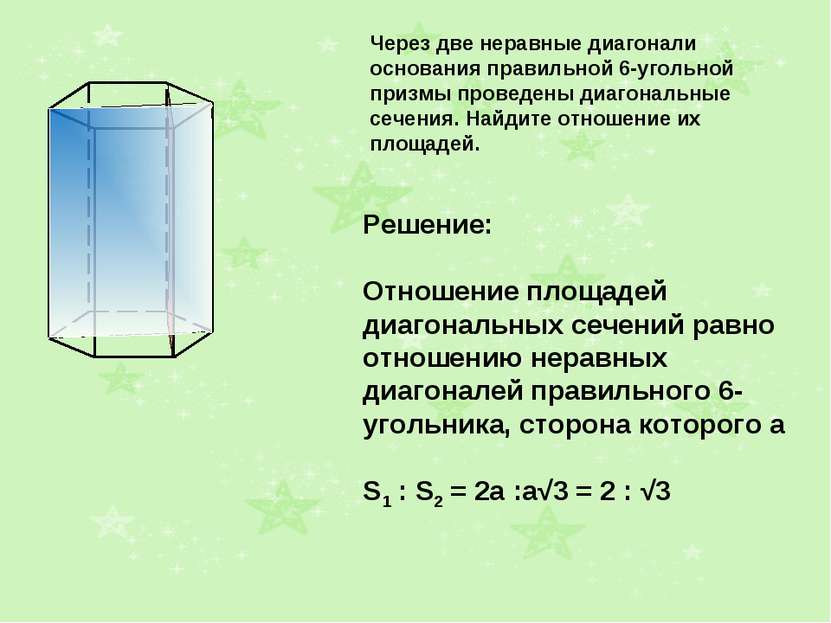
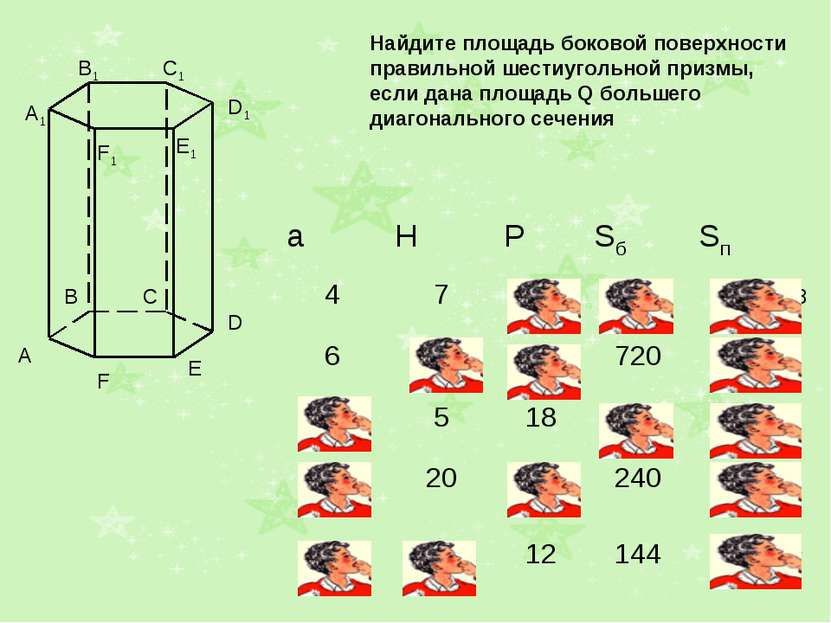
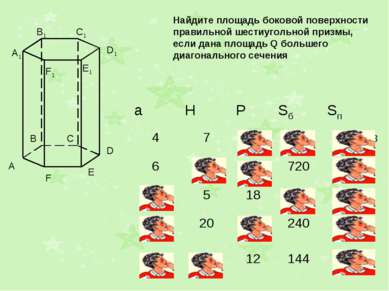
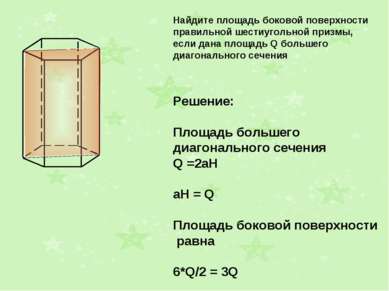Найдите площадь боковой поверхности правильной шестиугольной призмы, если дана площадь Q большего диагонального сечения Решение: Площадь большего диагонального сечения Q =2aH aH = Q Площадь боковой поверхности равна 6*Q/2 = 3Q
Cлайд 13
Через две неравные диагонали основания правильной 6-угольной призмы проведены диагональные сечения. Найдите отношение их площадей. Решение: Отношение площадей диагональных сечений равно отношению неравных диагоналей правильного 6-угольника, сторона которого а S1 : S2 = 2a :a√3 = 2 : √3
Cлайд 14
Найдите площадь боковой поверхности правильной шестиугольной призмы, если дана площадь Q большего диагонального сечения А1 В1 С1 D1 E1 F1 А В С D E F
