X
Код презентации скопируйте его
Пирамида, вписанная в конус
Скачать эту презентацию
Презентация на тему Пирамида, вписанная в конус
Скачать эту презентациюCлайд 1
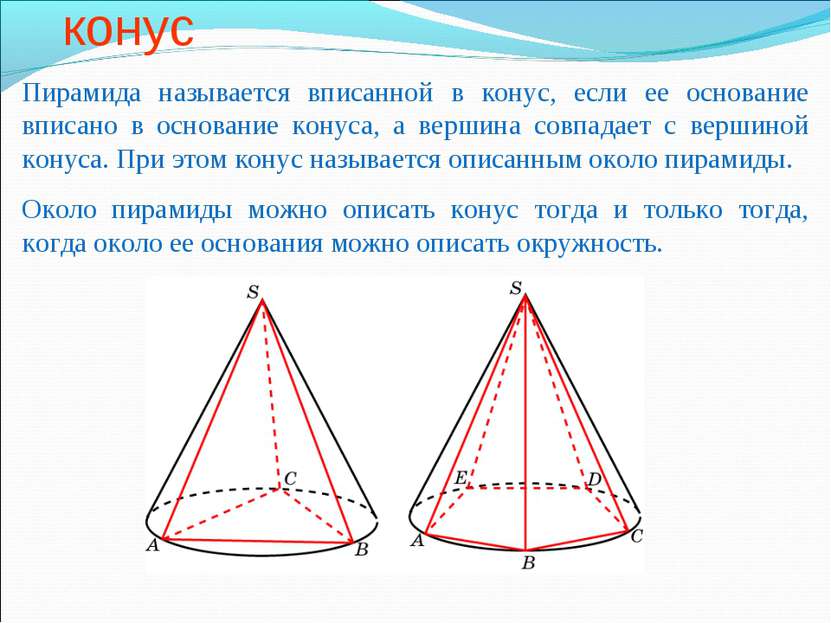
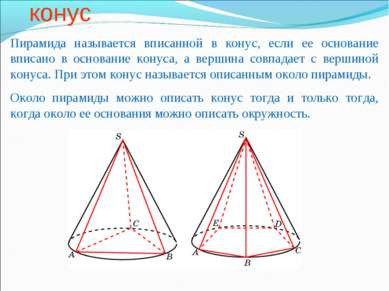Пирамида, вписанная в конус Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды. Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.
Cлайд 2
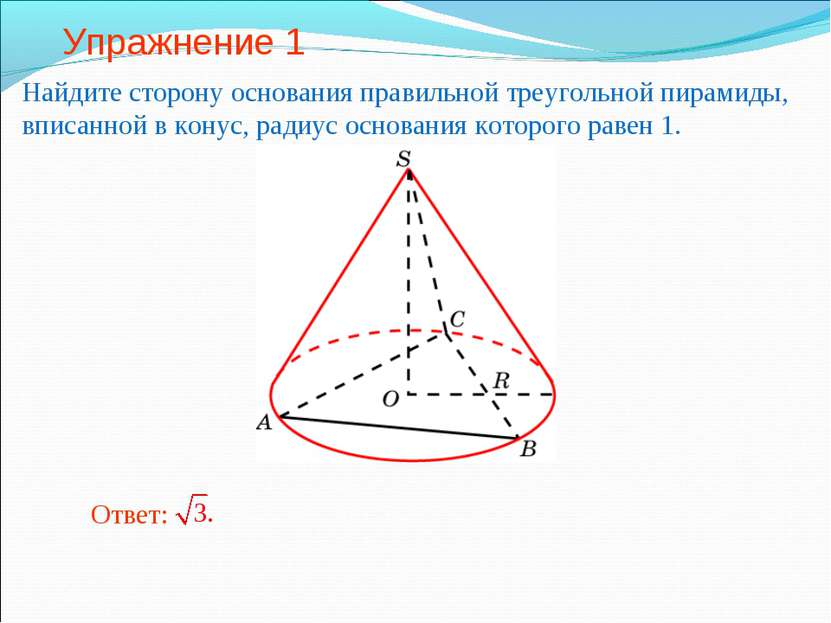
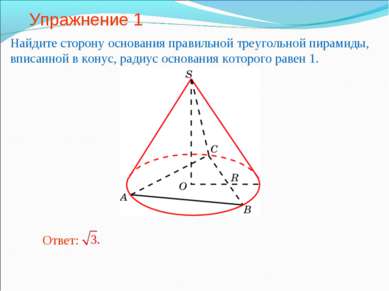Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Cлайд 3
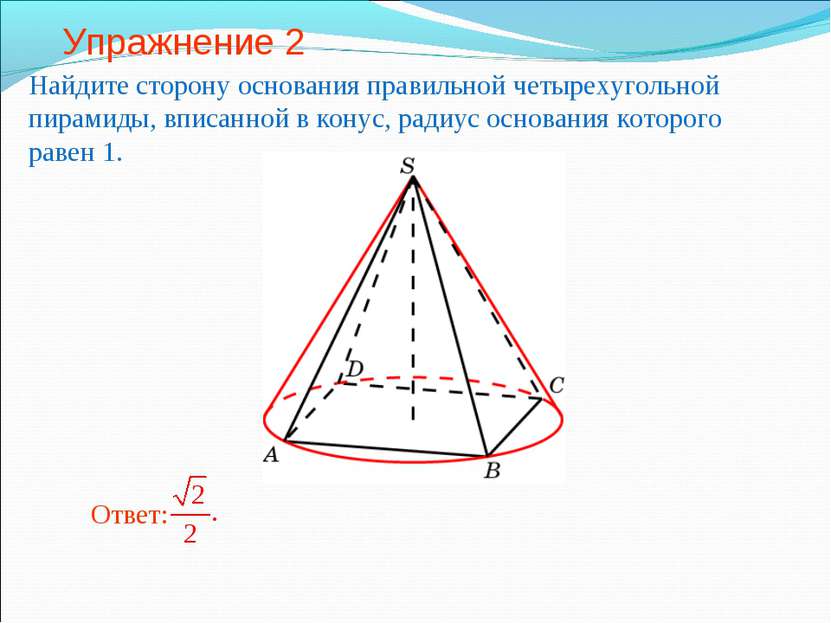
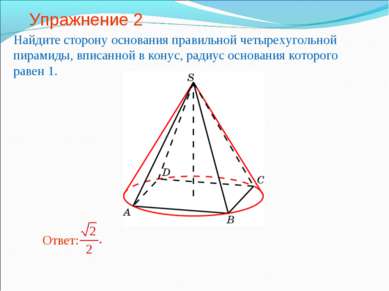Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Cлайд 4
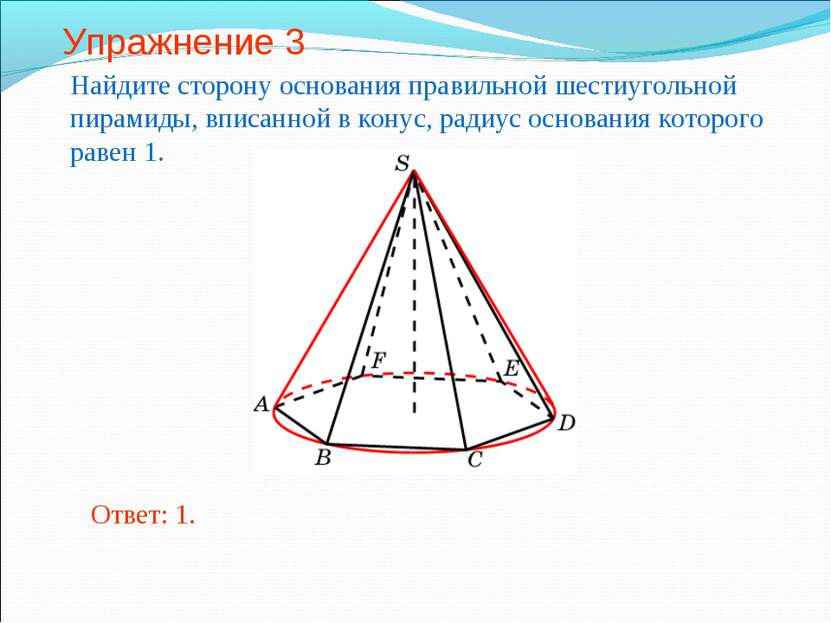
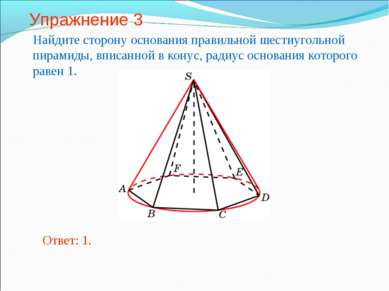Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1. Ответ: 1.
Cлайд 5
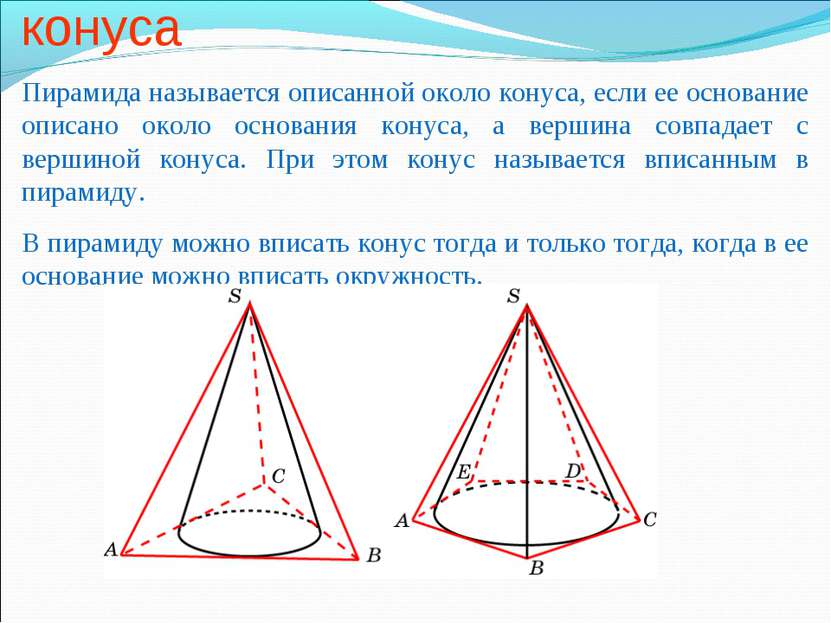
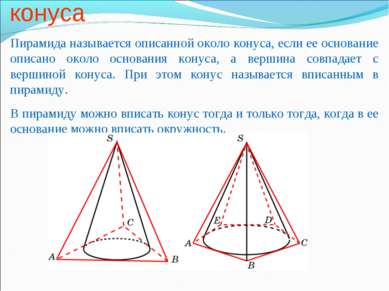Пирамида, описанная около конуса Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду. В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.
Cлайд 6
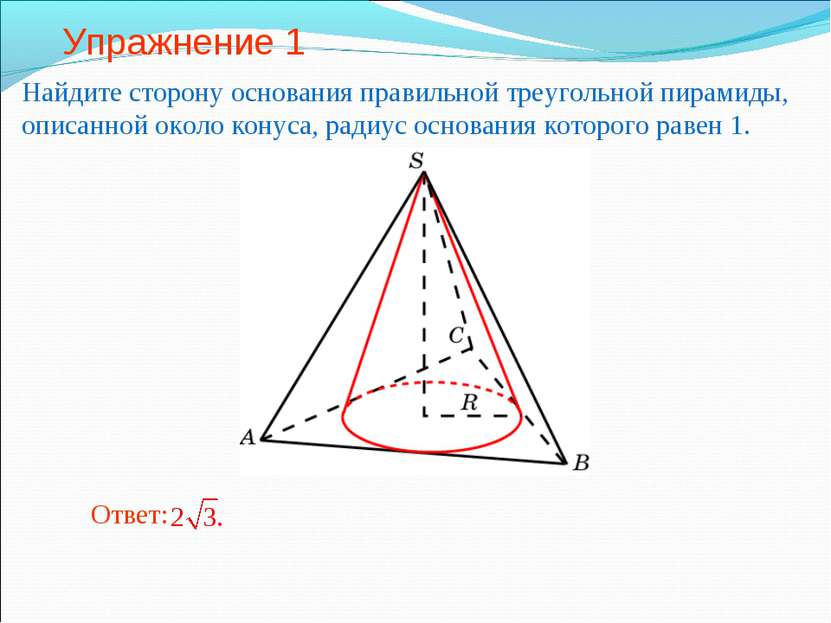
Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Cлайд 7
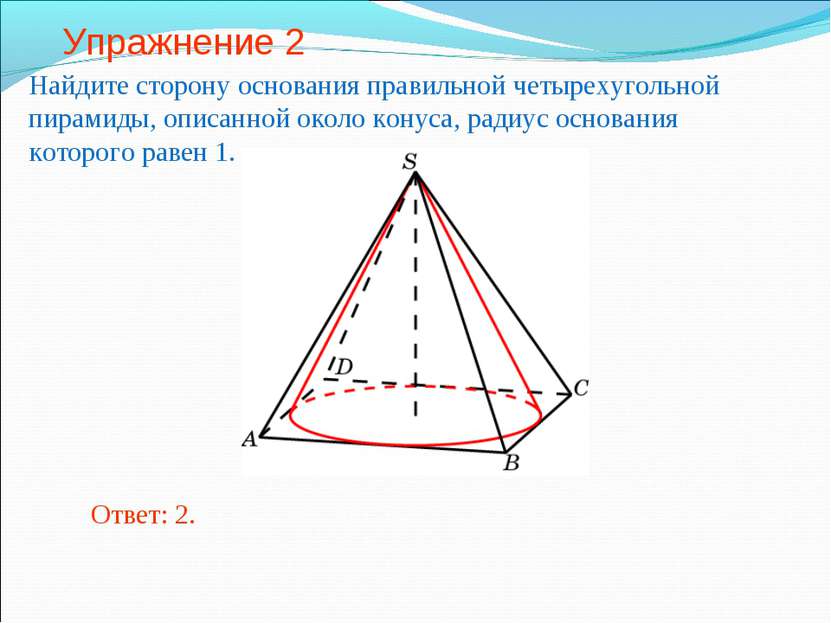
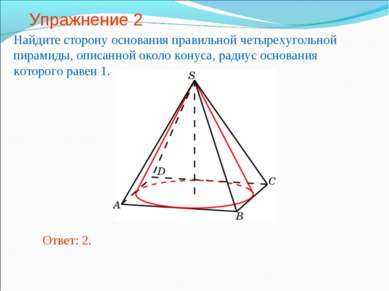Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1. Ответ: 2.
Cлайд 8
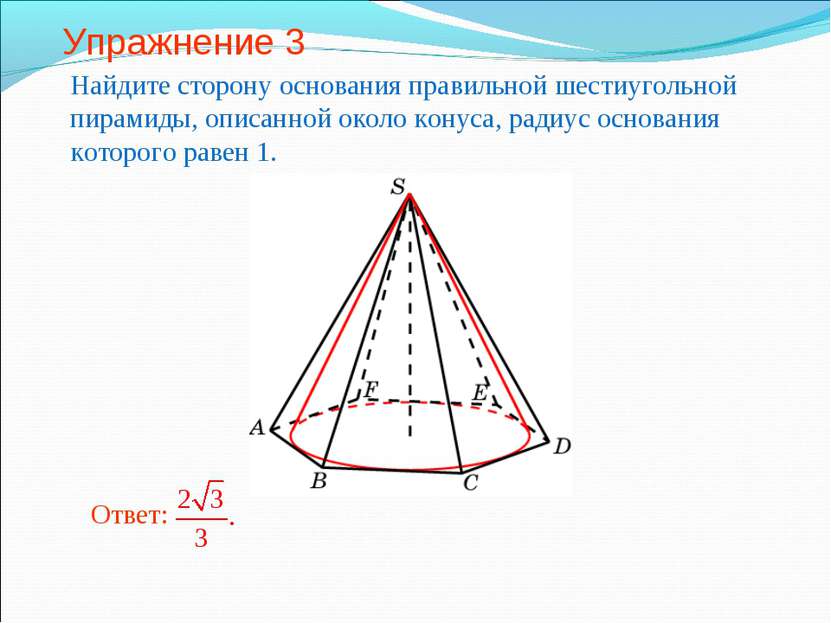
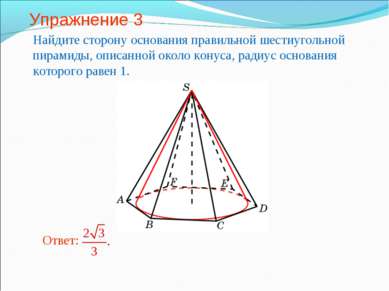Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Cлайд 9
Сфера, вписанная в конус Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы. В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса. Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле где S – площадь, p – полупериметр треугольника.
Cлайд 10
Упражнение 1 В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.
Cлайд 11
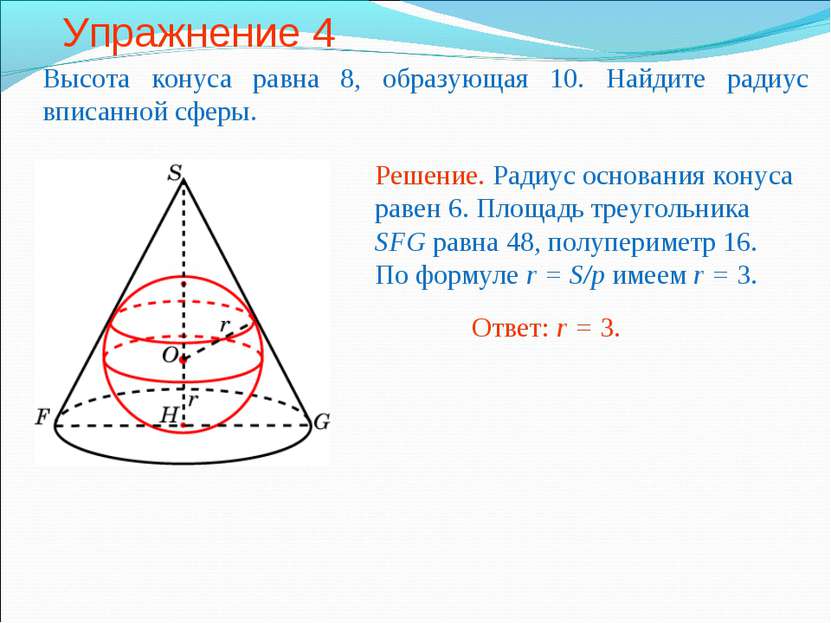
Упражнение 2 В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.
Cлайд 12
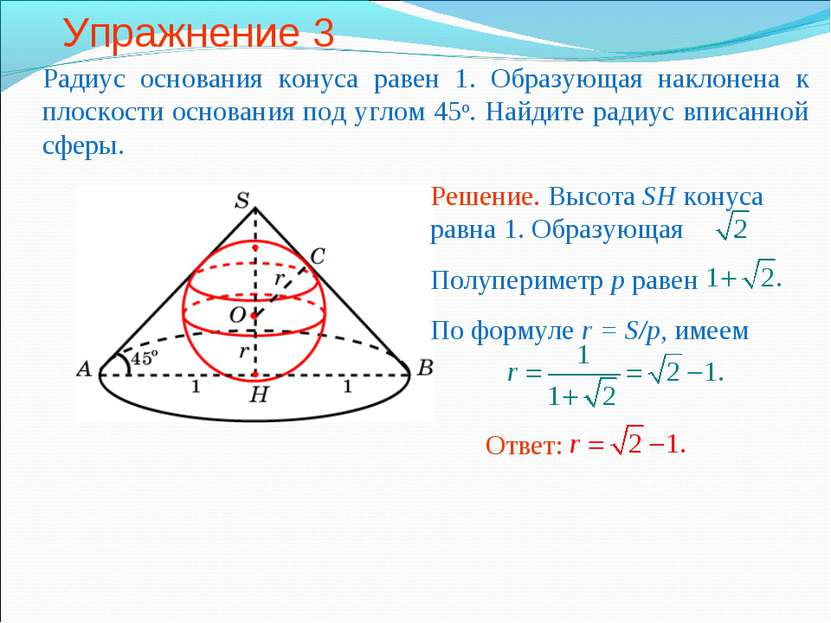
Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус вписанной сферы.
Cлайд 13
Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.
Cлайд 14
Упражнение 5 Можно ли вписать сферу в наклонный конус? Ответ: Нет.
Cлайд 15
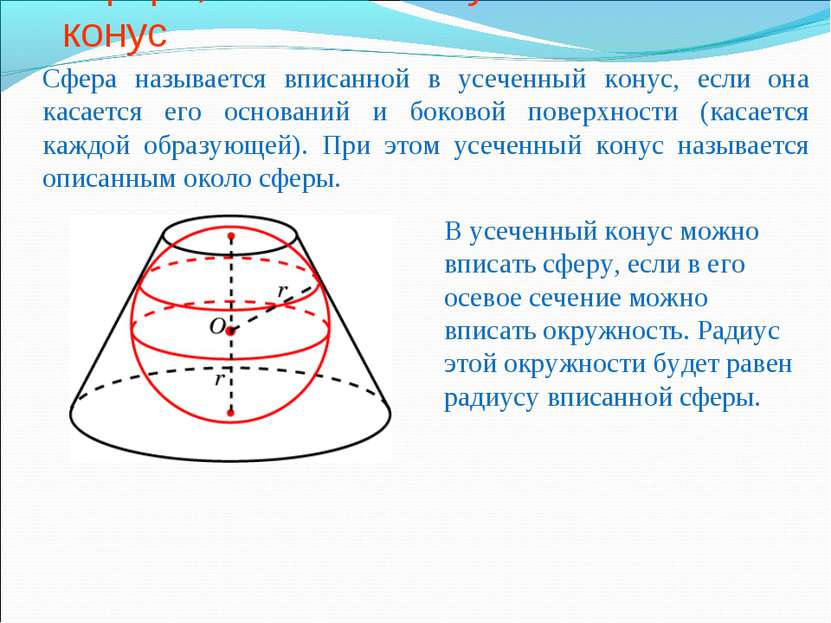
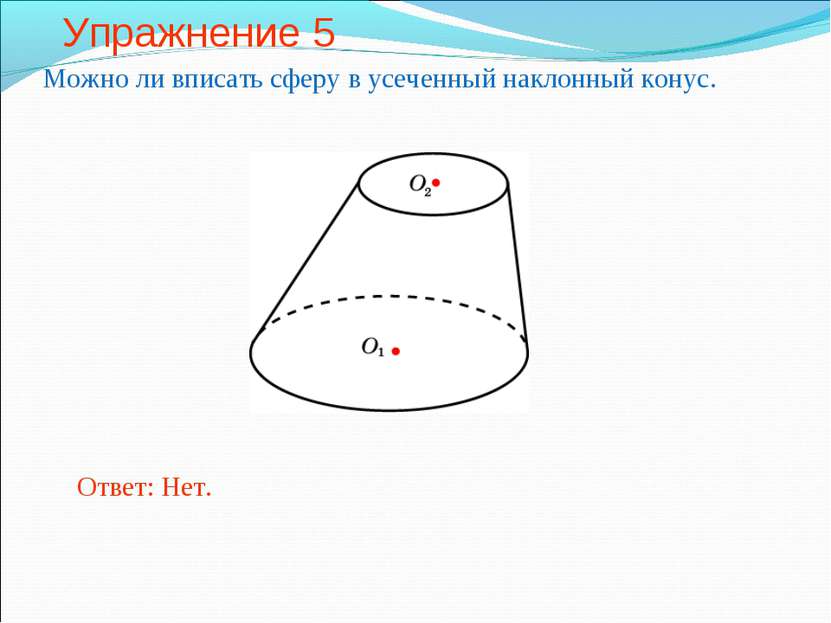
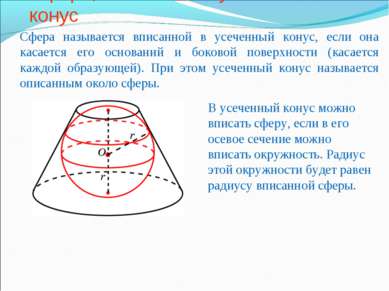Сфера, вписанная в усеченный конус Сфера называется вписанной в усеченный конус, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы. В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.
Cлайд 16
Упражнение 1 В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.
Cлайд 17
Упражнение 2 В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания. Решение. Пусть A1O1= 2. Обозначим r = A2O2. Имеем: A1A2 = 2+r, A1C = 2 – r. По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r, находим
Cлайд 18
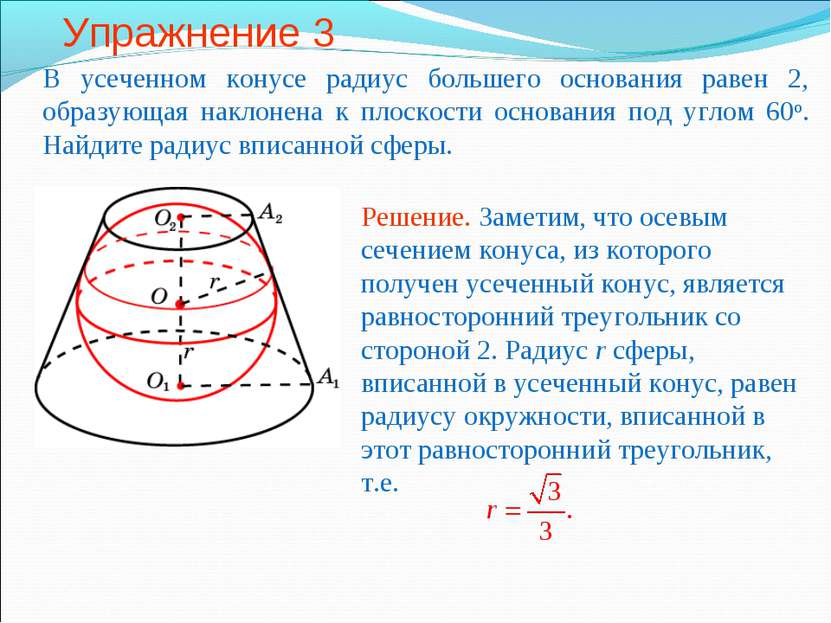
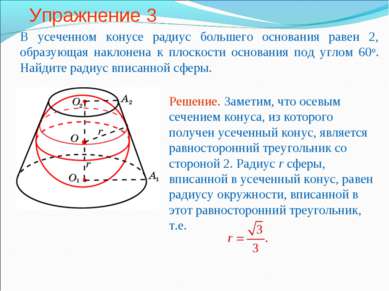Упражнение 3 В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60о. Найдите радиус вписанной сферы.
Cлайд 19
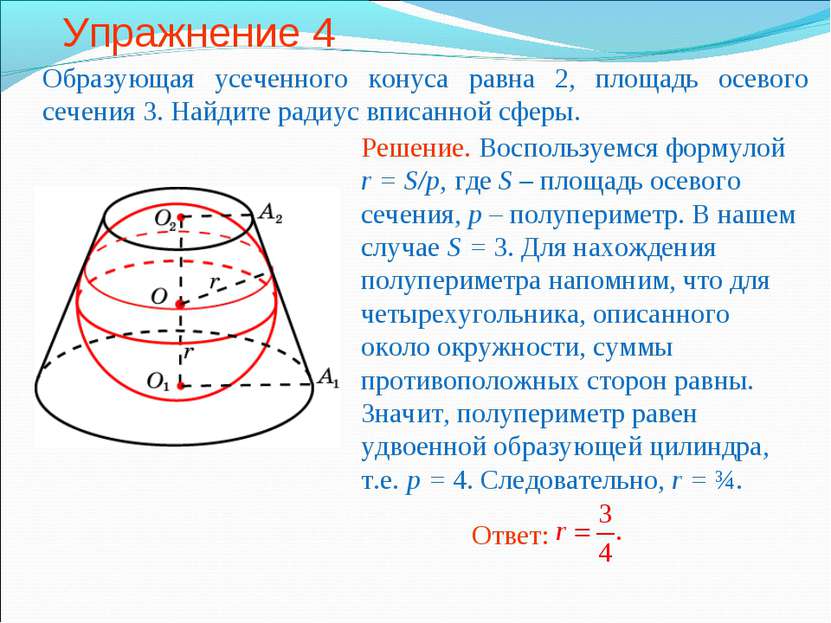
Упражнение 4 Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.
Cлайд 20
Упражнение 5 Можно ли вписать сферу в усеченный наклонный конус. Ответ: Нет.
Cлайд 21
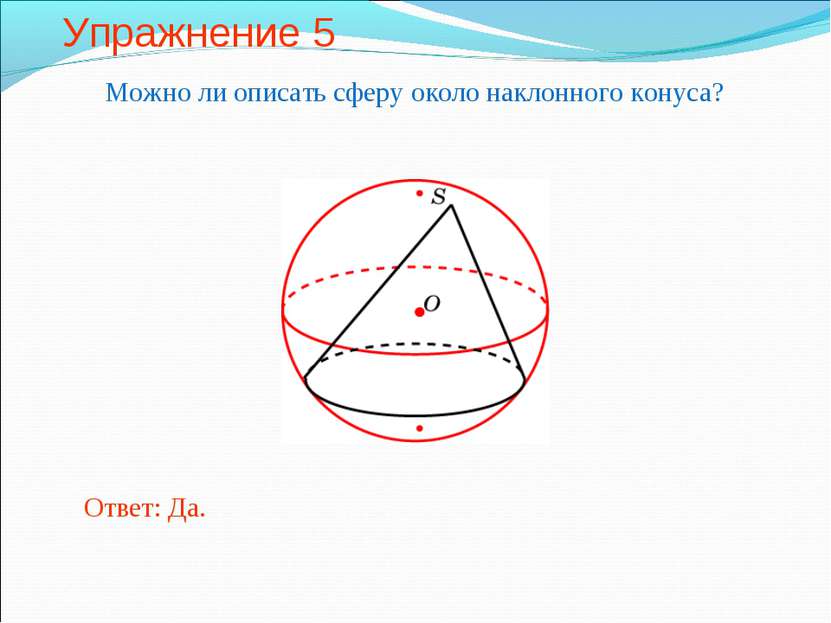
Сфера, описанная около конуса Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу. Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса. Напомним, что радиус R окружности, описанной около треугольника, находится по формуле где S – площадь, a, b, c – стороны треугольника.
Cлайд 22
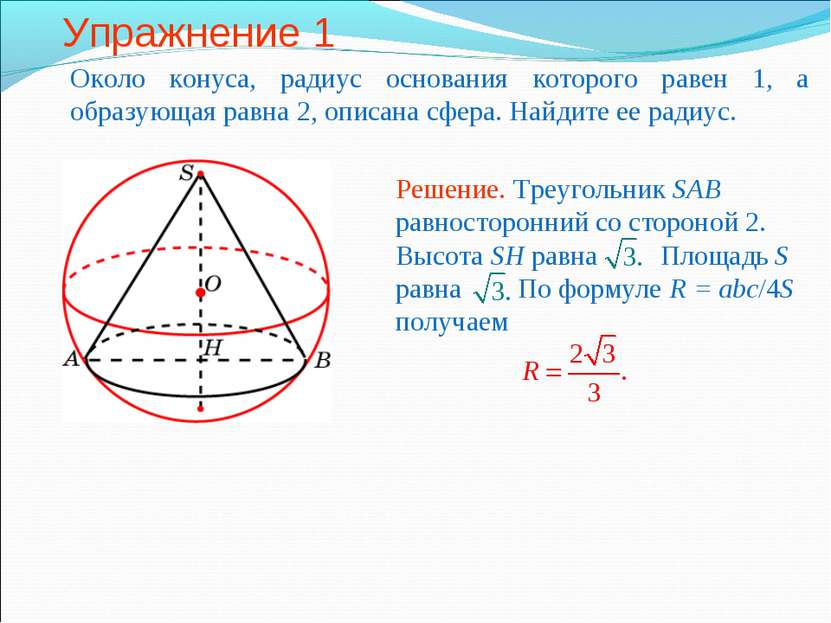
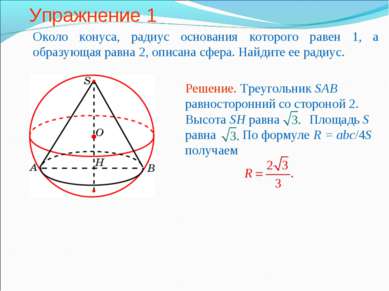Упражнение 1 Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Cлайд 23
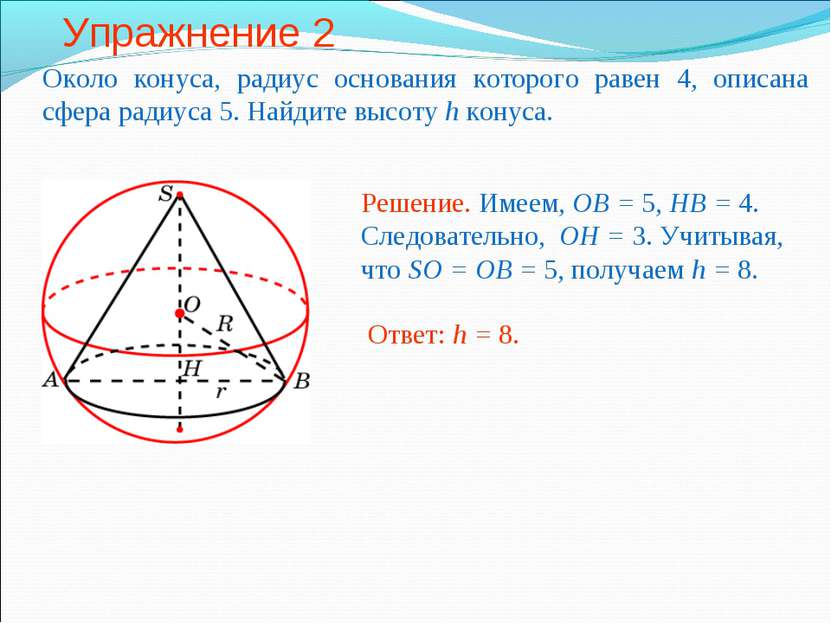
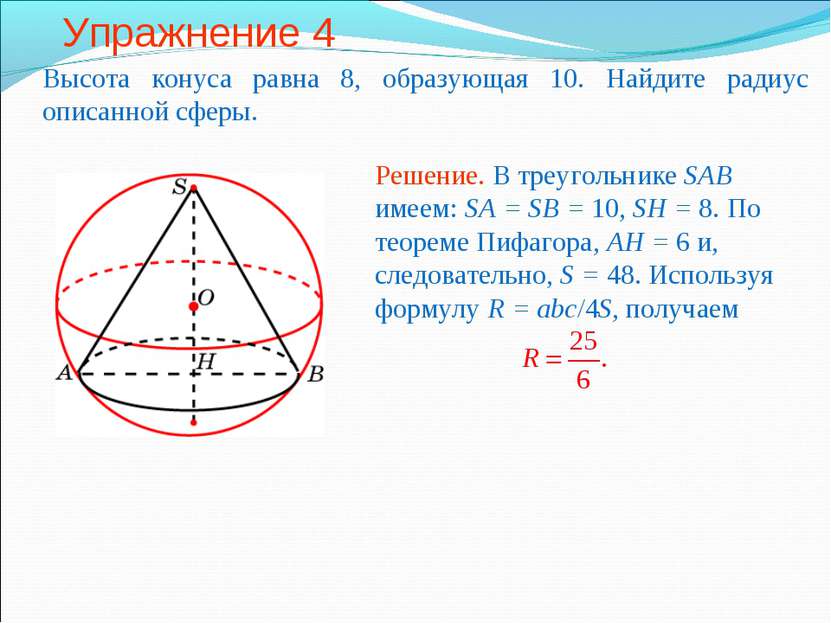
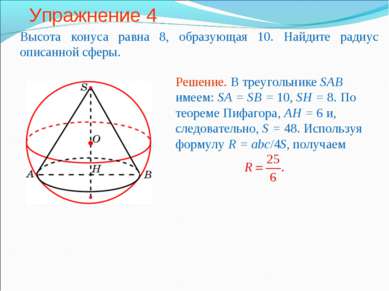
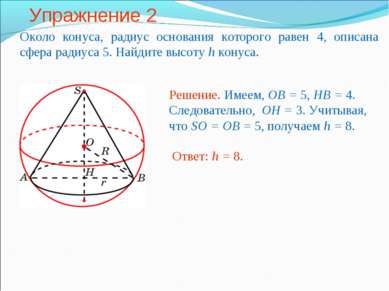Упражнение 2 Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.
Cлайд 24
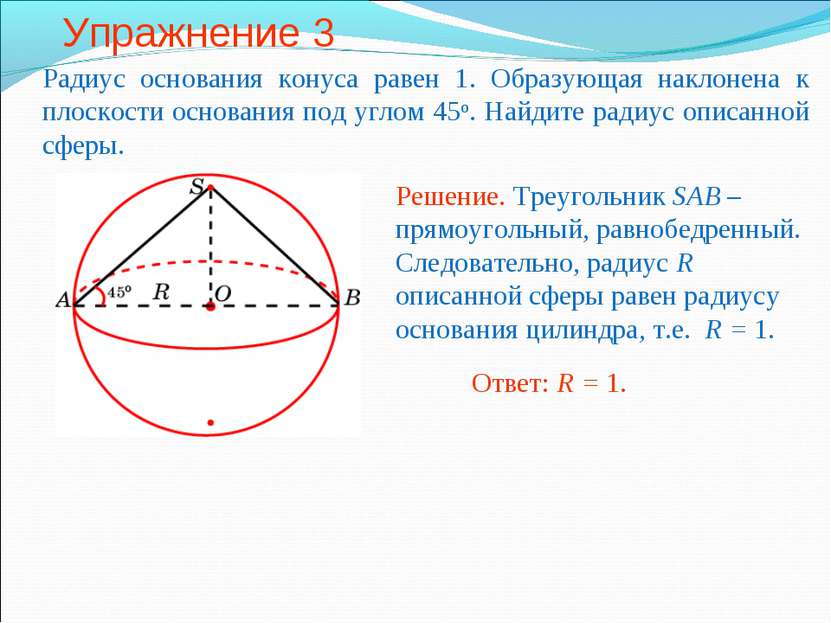
Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус описанной сферы.
Cлайд 25
Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.
Cлайд 26
Упражнение 5 Можно ли описать сферу около наклонного конуса?
Cлайд 27
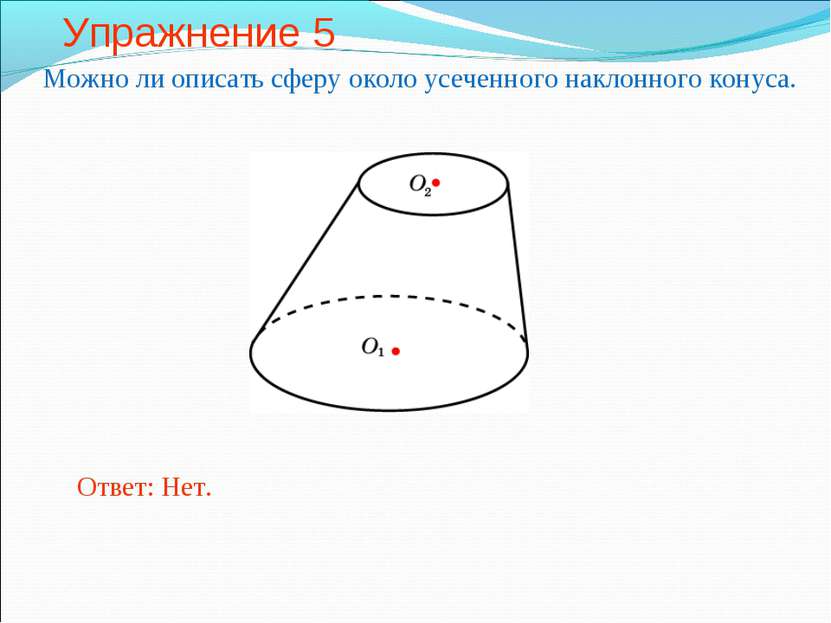
Сфера, описанная около усеченного конуса Сфера называется описанной около усеченного конуса, если окружности оснований усеченного конуса лежат на сфере. При этом усеченный конус называется вписанным в сферу. Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.
Cлайд 28
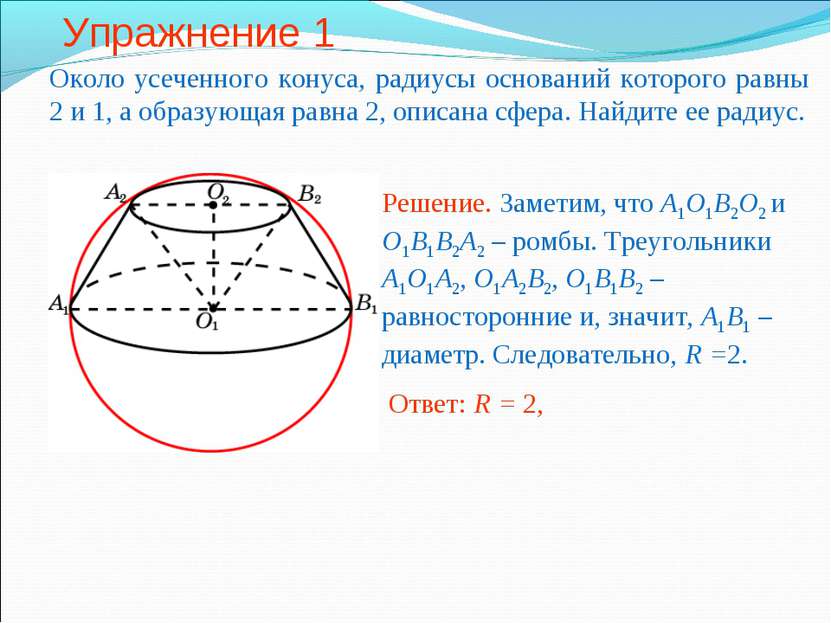
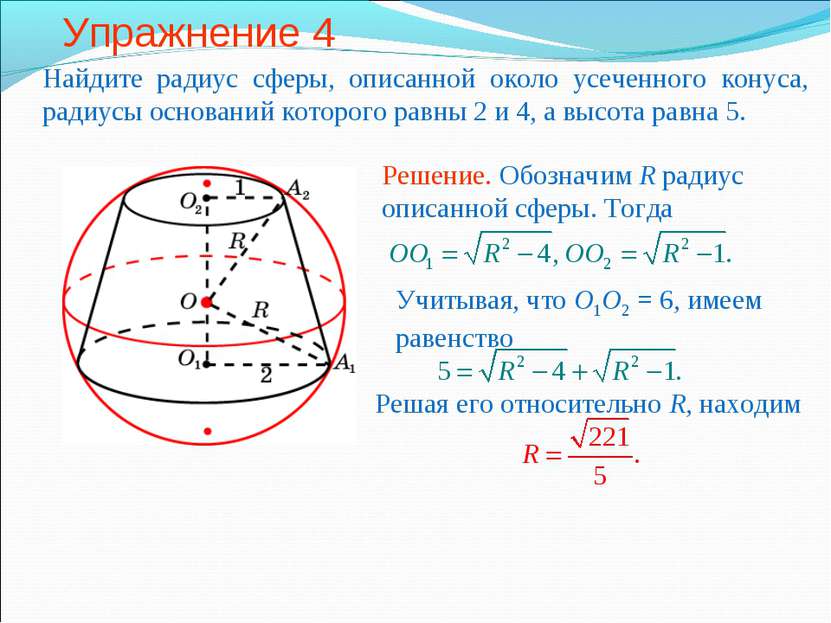
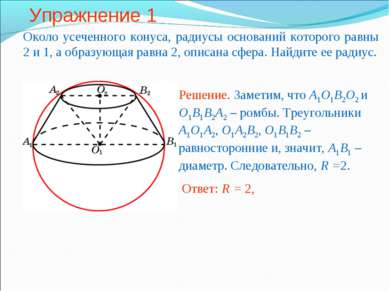Упражнение 1 Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Cлайд 29
Упражнение 2 Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45о с плоскостью другого основания. Найдите радиус описанной сферы.
Cлайд 30
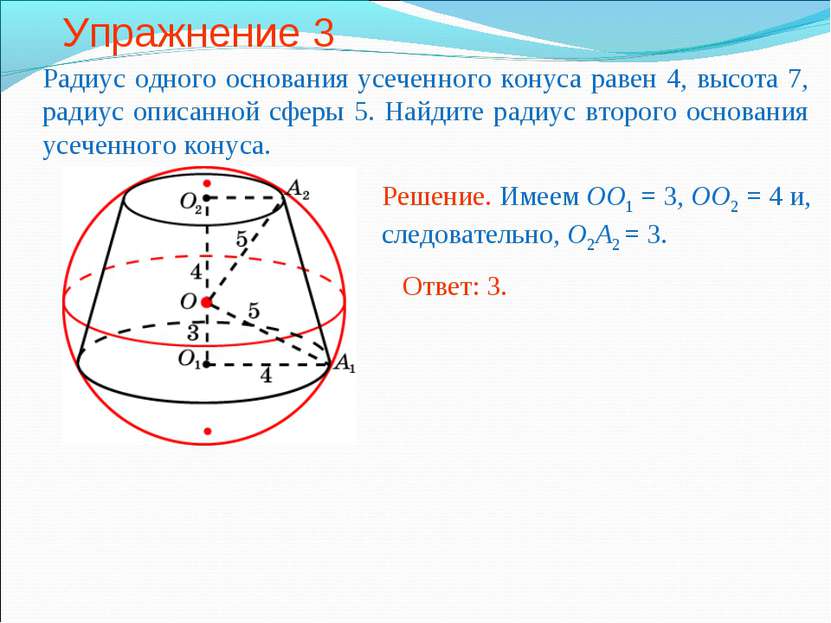
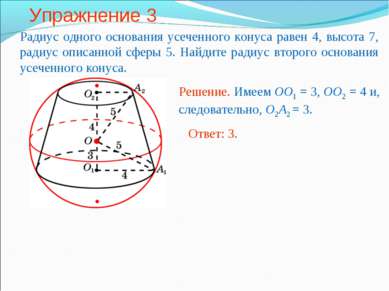Упражнение 3 Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.
Cлайд 31
Упражнение 4 Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.
Cлайд 32
Упражнение 5 Можно ли описать сферу около усеченного наклонного конуса. Ответ: Нет.
