X
Код презентации скопируйте его
Окружности
Скачать эту презентациюПрезентация на тему Окружности
Скачать эту презентациюCлайд 1
 Итоговое повторение планиметрии к ГИА. Выполнила Бородина Ульяна ученица 9Б класса. МОУ сош №5 г. Михайловки Волгоградской области.
Итоговое повторение планиметрии к ГИА. Выполнила Бородина Ульяна ученица 9Б класса. МОУ сош №5 г. Михайловки Волгоградской области.
Cлайд 2
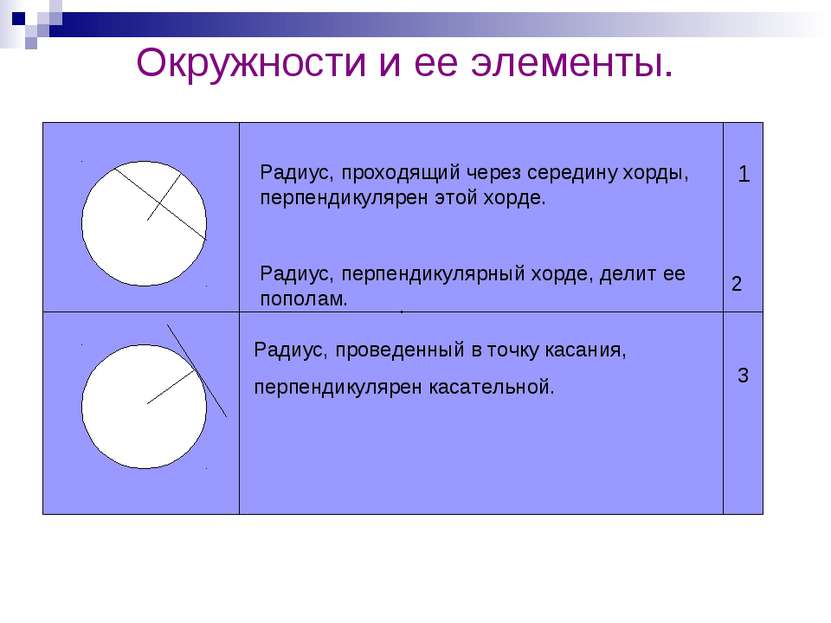
 Окружности и ее элементы. . Радиус, проходящий через середину хорды, перпендикулярен этой хорде. Радиус, перпендикулярный хорде, делит ее пополам. Радиус, проведенный в точку касания, перпендикулярен касательной. 1 3 2
Окружности и ее элементы. . Радиус, проходящий через середину хорды, перпендикулярен этой хорде. Радиус, перпендикулярный хорде, делит ее пополам. Радиус, проведенный в точку касания, перпендикулярен касательной. 1 3 2
Cлайд 3
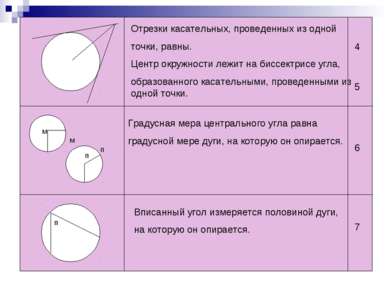 Отрезки касательных, проведенных из одной точки, равны. Центр окружности лежит на биссектрисе угла, образованного касательными, проведенными из одной точки. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается. Вписанный угол измеряется половиной дуги, на которую он опирается. п п п м м 4 5 6 7
Отрезки касательных, проведенных из одной точки, равны. Центр окружности лежит на биссектрисе угла, образованного касательными, проведенными из одной точки. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается. Вписанный угол измеряется половиной дуги, на которую он опирается. п п п м м 4 5 6 7
Cлайд 4
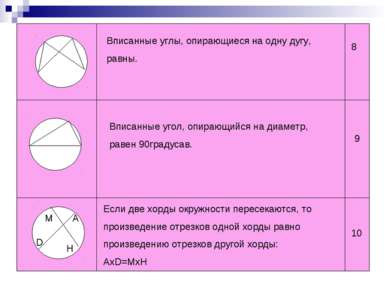 Вписанные углы, опирающиеся на одну дугу, равны. Вписанные угол, опирающийся на диаметр, равен 90градусав. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AxD=MxH М D H A 8 9 10
Вписанные углы, опирающиеся на одну дугу, равны. Вписанные угол, опирающийся на диаметр, равен 90градусав. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AxD=MxH М D H A 8 9 10
Cлайд 5
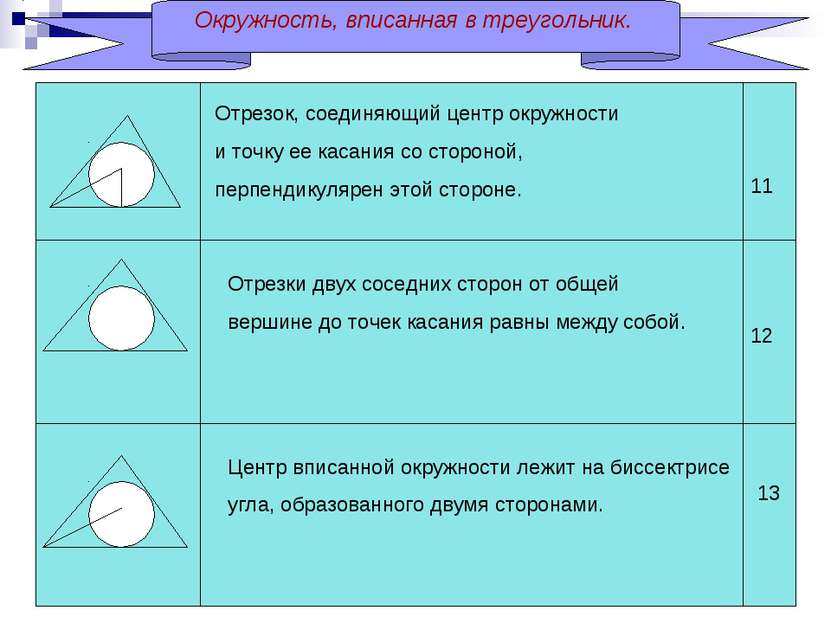
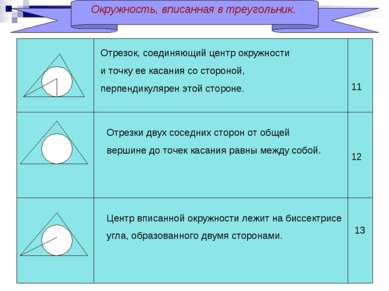 Окружность, вписанная в треугольник. Отрезок, соединяющий центр окружности и точку ее касания со стороной, перпендикулярен этой стороне. Отрезки двух соседних сторон от общей вершине до точек касания равны между собой. Центр вписанной окружности лежит на биссектрисе угла, образованного двумя сторонами. 11 12 13
Окружность, вписанная в треугольник. Отрезок, соединяющий центр окружности и точку ее касания со стороной, перпендикулярен этой стороне. Отрезки двух соседних сторон от общей вершине до точек касания равны между собой. Центр вписанной окружности лежит на биссектрисе угла, образованного двумя сторонами. 11 12 13
Cлайд 6
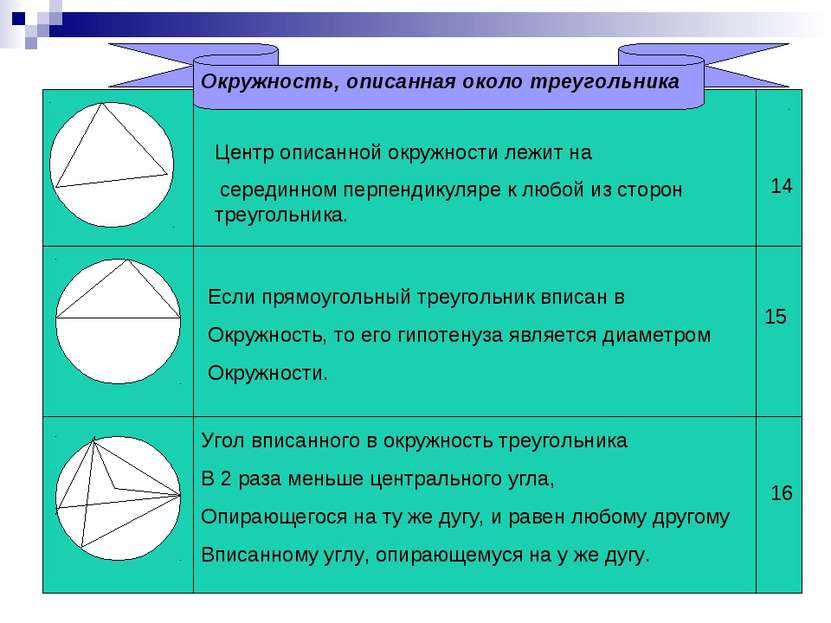
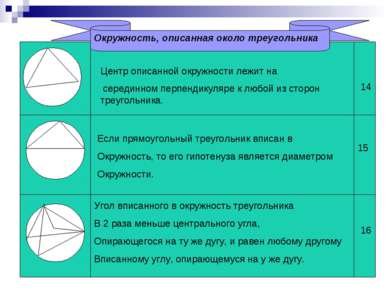 Окружность, описанная около треугольника Центр описанной окружности лежит на серединном перпендикуляре к любой из сторон треугольника. Если прямоугольный треугольник вписан в Окружность, то его гипотенуза является диаметром Окружности. Угол вписанного в окружность треугольника В 2 раза меньше центрального угла, Опирающегося на ту же дугу, и равен любому другому Вписанному углу, опирающемуся на у же дугу. 14 15 16
Окружность, описанная около треугольника Центр описанной окружности лежит на серединном перпендикуляре к любой из сторон треугольника. Если прямоугольный треугольник вписан в Окружность, то его гипотенуза является диаметром Окружности. Угол вписанного в окружность треугольника В 2 раза меньше центрального угла, Опирающегося на ту же дугу, и равен любому другому Вписанному углу, опирающемуся на у же дугу. 14 15 16
Cлайд 7
 Из точки А к окружности с центром О проведены касательные АВ с АС. Отрезки АО и ВС пересекаются в точке К. Найдите радиус окружности, если ВС=6, АК=2,25. О В С А Т.к АБС- равнобедренный, а АК- его биссектриса(4),(5),то АК ВС и ВК=СК=3 Проведем радиус ОВ, тогда АОВ- прямоугольный, ВК- его высота. Тогда ВКxВК=ОКxАК, откуда ОК=9:2,25=9:(9:4)=4. Ответ:4
Из точки А к окружности с центром О проведены касательные АВ с АС. Отрезки АО и ВС пересекаются в точке К. Найдите радиус окружности, если ВС=6, АК=2,25. О В С А Т.к АБС- равнобедренный, а АК- его биссектриса(4),(5),то АК ВС и ВК=СК=3 Проведем радиус ОВ, тогда АОВ- прямоугольный, ВК- его высота. Тогда ВКxВК=ОКxАК, откуда ОК=9:2,25=9:(9:4)=4. Ответ:4
Cлайд 8
 В прямоугольном треугольнике АВС угол С прямой, О- центр вписанной окружности, ОВ=12, угол ВОС=105. найдите радиус вписанной окружности. СО- Биссектриса угла С (13), значит, угол ОСВ=45 Тогда ОВС= 180-45-105=30 2)Проведем из центра О радиус р в точку касания с катетом ВС, тогда р паралельно ВС(11), то есть ВОН-прямоугольный. 3) р = ОВ:2, р=6. Ответ:6 А В О С Н 2р р
В прямоугольном треугольнике АВС угол С прямой, О- центр вписанной окружности, ОВ=12, угол ВОС=105. найдите радиус вписанной окружности. СО- Биссектриса угла С (13), значит, угол ОСВ=45 Тогда ОВС= 180-45-105=30 2)Проведем из центра О радиус р в точку касания с катетом ВС, тогда р паралельно ВС(11), то есть ВОН-прямоугольный. 3) р = ОВ:2, р=6. Ответ:6 А В О С Н 2р р