X
Код презентации скопируйте его
Определение синуса, косинуса, тангенса и котангенса
Скачать эту презентацию
Презентация на тему Определение синуса, косинуса, тангенса и котангенса
Скачать эту презентациюCлайд 1
Тема: Определение синуса, косинуса, тангенса и котангенса.
Cлайд 2
Цели урока: 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров и задач. 3.Привитие творческой активности и самостоятель-ности
Cлайд 3
План урока История развития тригонометрии. Повторение курса геометрии. Изучение нового материала. Закрепление
Cлайд 4
Историческая справка тригонон Тригонометрия метрио (измерение треугольника)
Cлайд 5
Древний Вавилон-умели предсказывать солнечные и лунные затмения. Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы) Учёные Индии и Ближнего Востока-положили начало радианной мере угла.
Cлайд 6
Большой вклад в развитие тригонометрии внесли: Гиппарх Птолемей Франсуа Виет Эйлер Бернулли
Cлайд 7
Повторение А sinC= COS C= tg C= В С ?
Cлайд 8
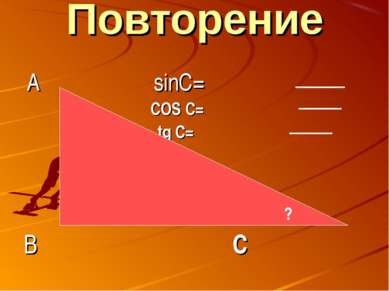
Повторение Для единичной полуокружности y у SIN A = = Y R X COS A= = X R 0 ≤SIN A≤ 1 -1 ≤ COS A ≤1 х А В 1 -1 1
Cлайд 9
Повторение Основное тригонометрическое тождество: SIN2 X+COS2 Х=1
Cлайд 10
у х А О
Cлайд 11
Угол поворота против часовой стрелки- положительный А О В У Х
Cлайд 12
Угол поворота по часовой стрелке - отрицательный О х У А В
Cлайд 13
Угол поворота Положительный Отрицательный В А А В 700 -700 Х У У Х o O
Cлайд 14
Из курса геометрии известно: Мера угла в градусах выражается числом от 00 до 1800
Cлайд 15
Ответь на вопрос: Каким числом может выражаться в градусах угол поворота?
Cлайд 16
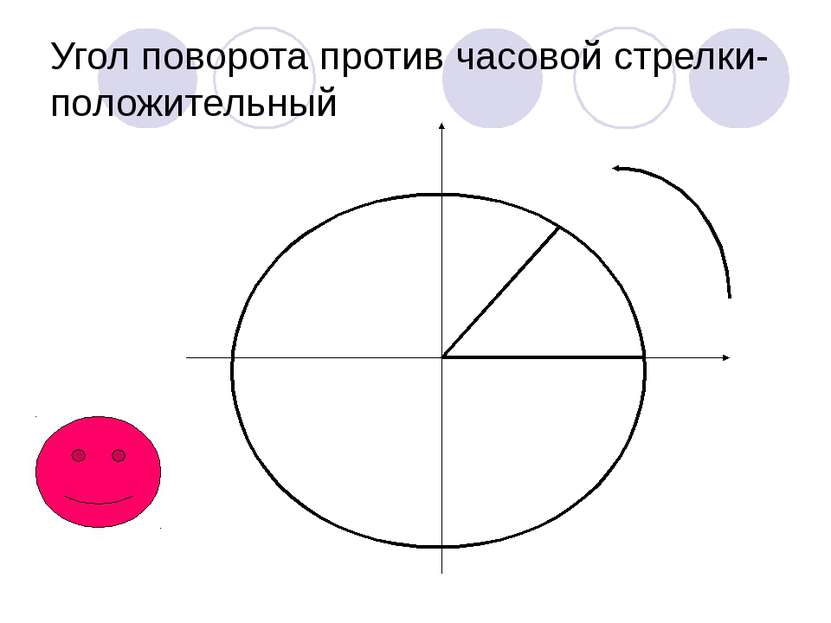
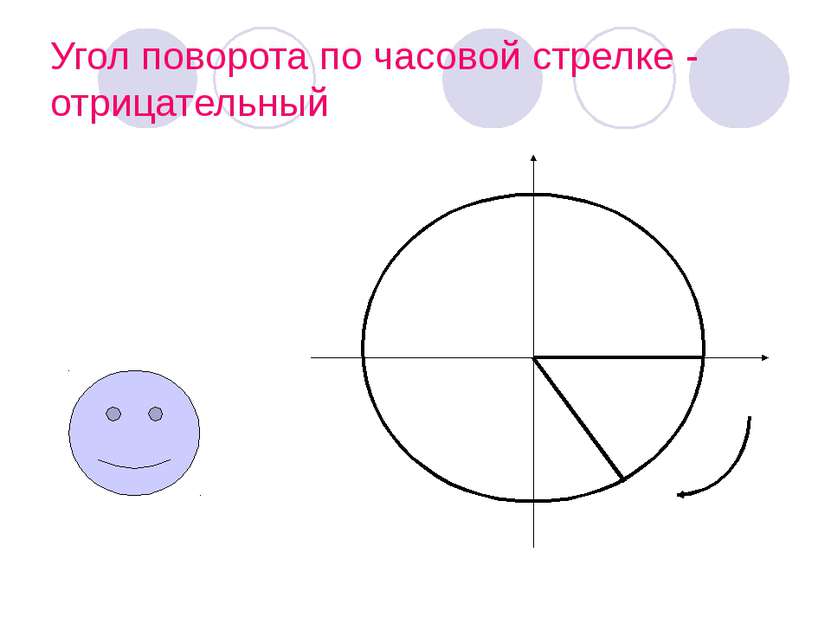
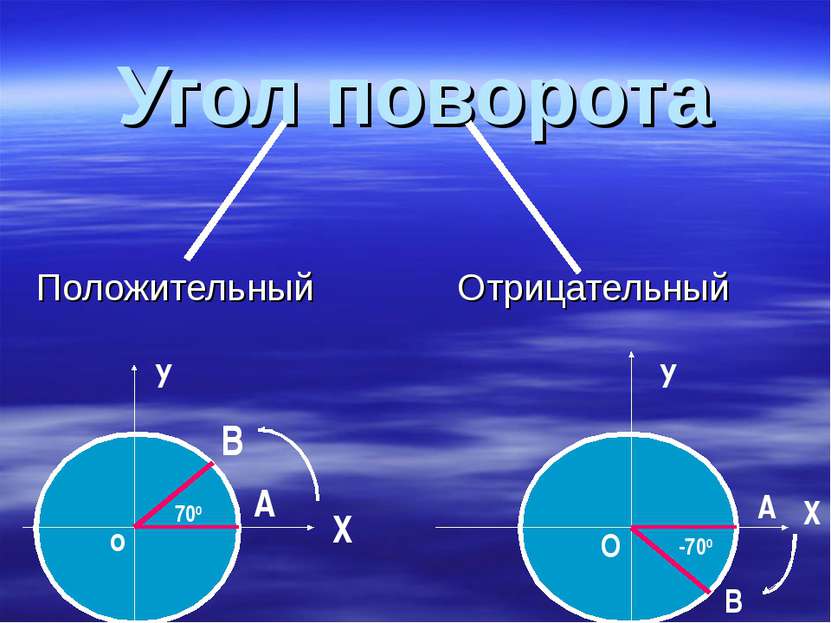
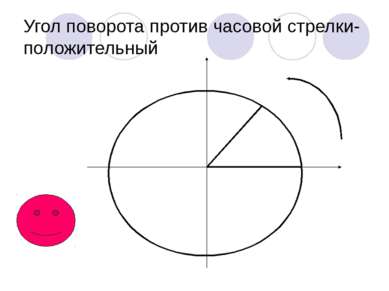
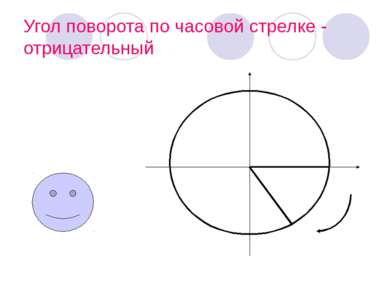
В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от -∞ до +∞
Cлайд 17
Рассмотрим примеры 1350+3600n , n=0,1,-1,2,-2….. 1350 Х У У Х -1350 А В О В О А
Cлайд 18
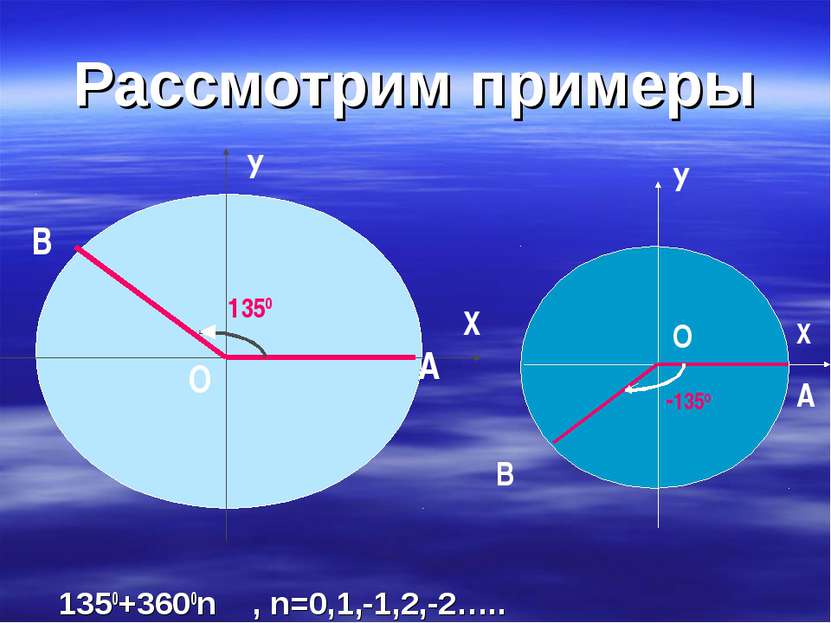
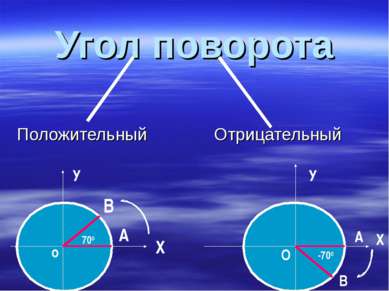
В Ы В О Д Существует бесконечно много углов поворота, при которых начальный радиус ОА переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол α называют углом этой четверти.
Cлайд 19
З А П О М Н И 00
Cлайд 20
В ы в о д: Эти углы не относятся ни к какой четверти. 00 ,± 900 ,± 1800 , ± 2700 ,± 3600....
Cлайд 21
Углом какой четверти является угол β,если: β=1670 β=2870 β=-650
Cлайд 22
Стр.153.- определение. y X Sinα= Cos= R R y X tgα= ctgα= X y
Cлайд 23
Лабораторная работа
Cлайд 24
В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса. Вычертите три окружности произвольного радиуса с центром в начале координат. Постройте начальный радиус ОА. Поверните начальный радиус на угол α=450 В каждом из случаев найдите SIN 450. (смотри пример 1. стр.154.) Какой получился результат? Сделай вывод..
Cлайд 25
Запомни Sinα, Cosα-определены при любом α. Почему?
Cлайд 26
Стр.154 При каком α tgα не определён? Почему?
Cлайд 27
sinα , cosα , tgα , ctgα –называют тригонометрическими функциями.
Cлайд 28
Для единичной окружности: Область значения синуса и косинуса есть промежуток [-1;1] Область значения тангенса и котангенса есть множество всех действительных чисел.
Cлайд 29
Найти синус, косинус,тангенс и котангенс 2700 Проверьте решение на стр.156
Cлайд 30
Устно № 699 №701
Cлайд 31
Письменно №705 Используй таблицу стр.155
