X
Код презентации скопируйте его
Объёмы тел
Скачать эту презентацию
Презентация на тему Объёмы тел
Скачать эту презентациюCлайд 1
МБОУ СОШ с. Камышки Тема : «Объёмы тел» Учитель: Мурзагалиева Акмоншак Хасеновна.
Cлайд 2
Если бы я родился музыкантом, Я бы стремился перебороть шумы мира С помощью стройных звуков. Если бы я родился архитектором, Я бы строил людям не квартиры, а домашние очаги. Я одарил бы их светом, цветом и тишиной, Но поскольку я поэт, Я хотел бы так же четко и ясно Говорить на языке слов, Как математики говорят на языке чисел.
Cлайд 3
Объёмы тел
Cлайд 4
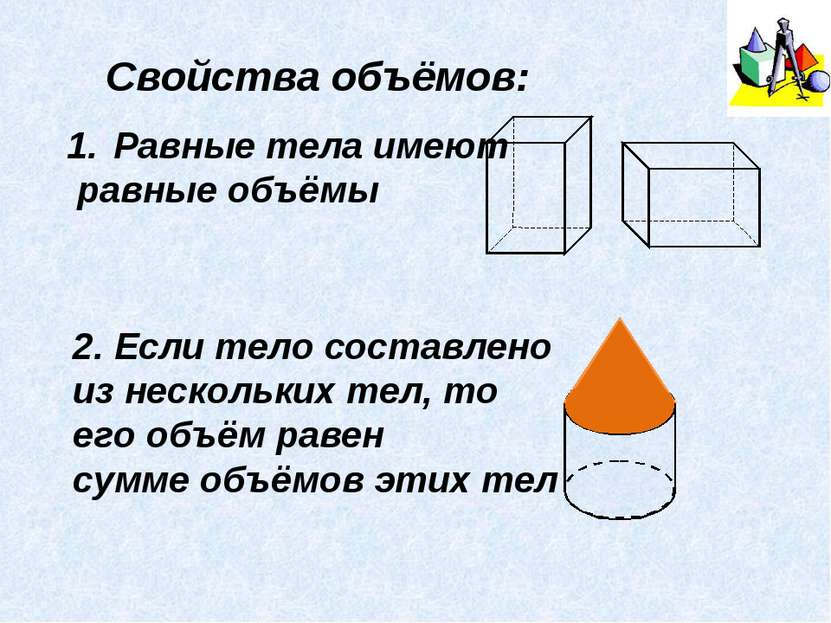
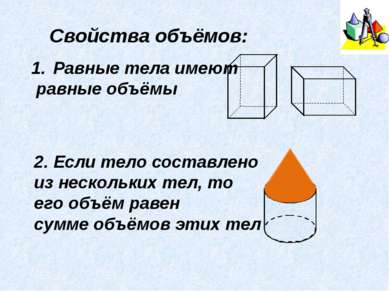
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами
Cлайд 5
Свойства объёмов: Равные тела имеют равные объёмы
Cлайд 6
Симпсон Томас - английский математик. В 1743 вывел формулу приближённого интегрирования. В 1746 году Симпсон избран в члены Лондонского королевского общества, а ранее — в члены основанного в 1717 году в Лондоне Математического общества. Назначенный профессором в Вульвич, Симсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи.
Cлайд 7
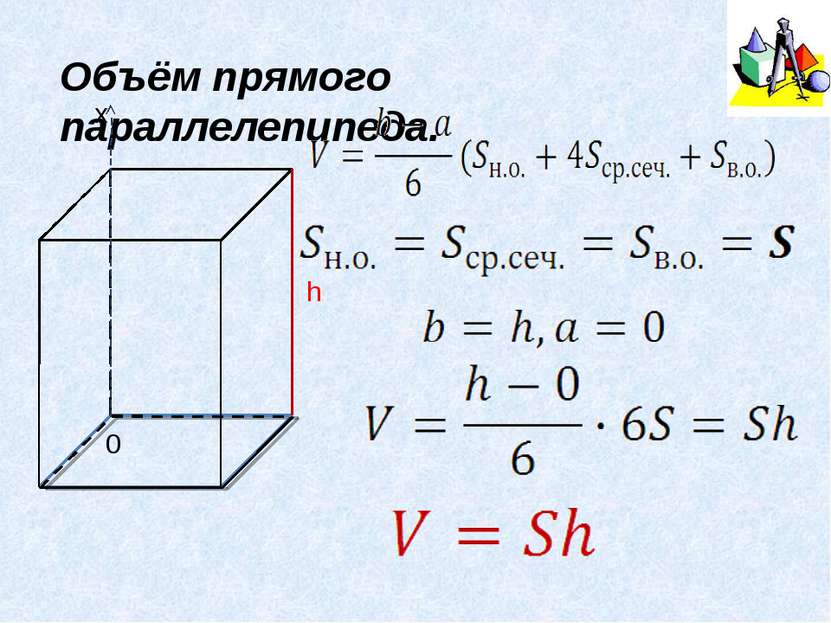
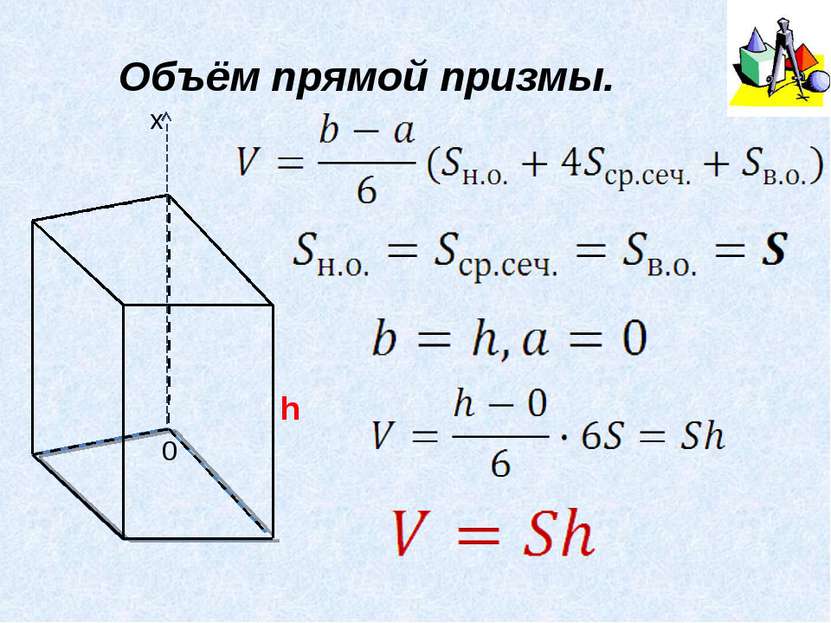
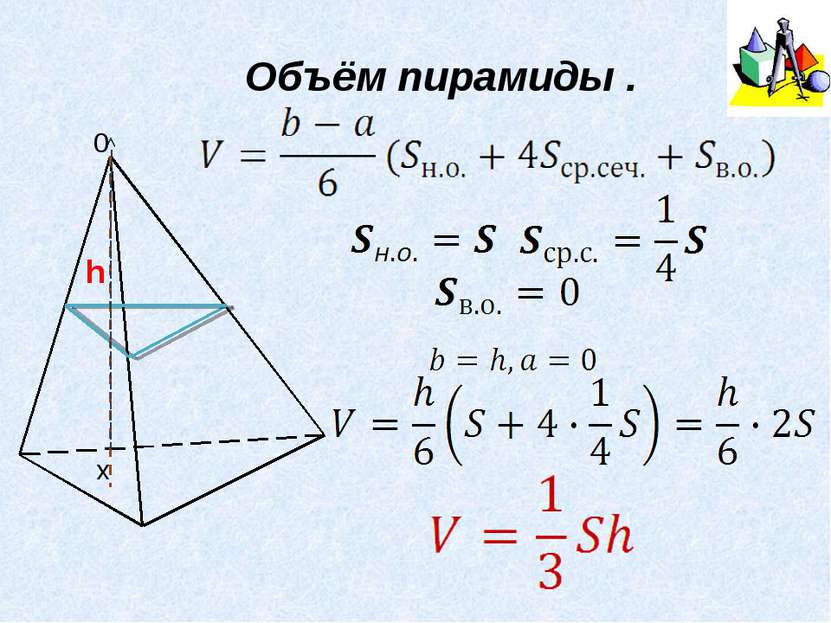
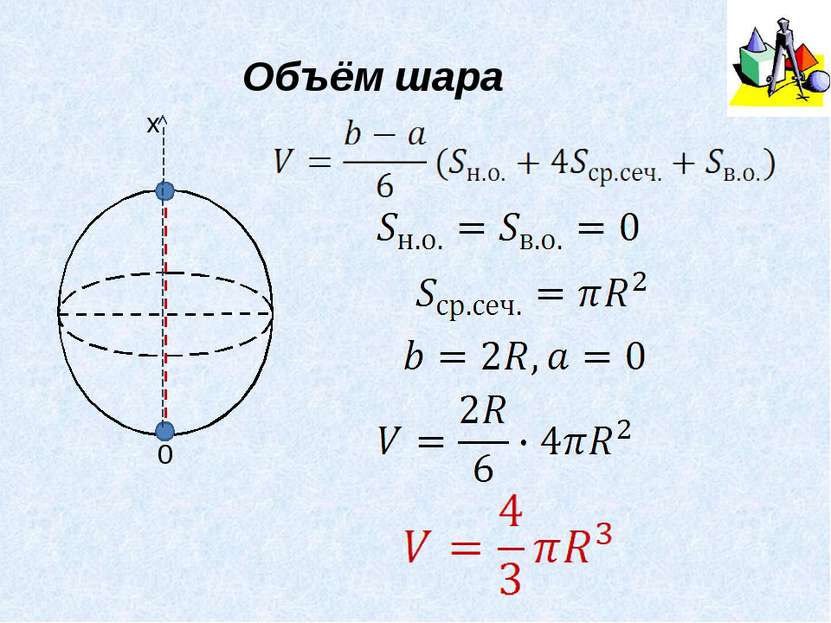
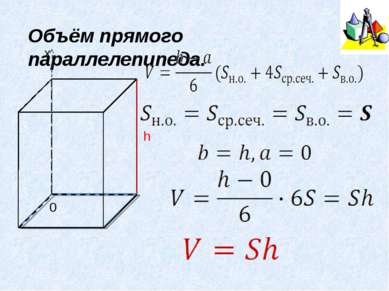
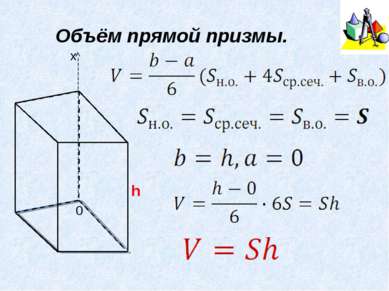
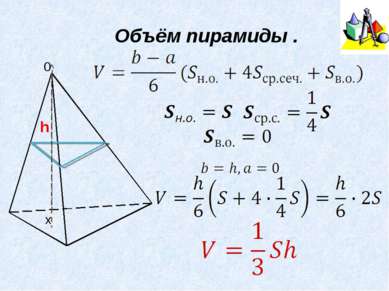
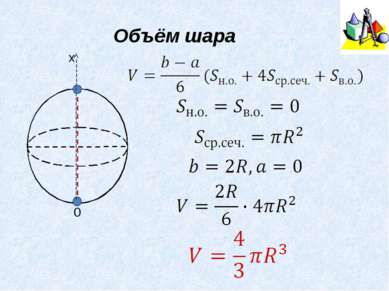
Формула Симпсона b, a – предельные значения высоты геометрического тела, среднее сечение – сечение тела плоскостью, параллельной основанию, и проходящей через середину высоты
Cлайд 8
Как найти объем у куба? Есть у куба 3 стены, В них по три величины. Я возьму их, перемножу. Ведь не так все это сложно. С первой стенки взял длину, Со второй взял ширину, С третьей вышла высота. Получилась красота!
Cлайд 9
Объём прямого параллелепипеда. h
Cлайд 10
Объём прямой призмы. h
Cлайд 11
-Цилиндр, что такое? - спросил я у папы. Отец рассмеялся : - Цилиндр, это шляпа. Чтобы иметь представление верное, Цилиндр, скажем так, это банка консервная. Труба парохода- цилиндр, Труба на нашей крыше - тоже, Все трубы на цилиндр похожи. А я привёл пример такой - Калейдоскоп любимый мой, Глаз от него не оторвёшь, И тоже на цилиндр похож.
Cлайд 12
Объём цилиндра. h
Cлайд 13
Я видел картину. На этой картине Стоит ПИРАМИДА в песчаной пустыне. Всё в пирамиде необычайно, Какая-то есть в ней загадка и тайна. А Спасская башня на площади Красной И детям, и взрослым знакома прекрасно. Посмотришь на башню, обычная с виду, А что на вершине у ней? Пирамида!
Cлайд 14
Объём пирамиды .
Cлайд 15
Сказала мама: - А сейчас Про конус будет мой рассказ. В высокой шапке звездочёт Считает звёзды круглый год. КОНУС- шляпа звездочёта. Вот какой он. Понял? То-то. Мама у стола стояла В бутылки масло разливала. - Где воронка? Нет воронки. Поищи. Не стой в сторонке. -Мама, с места я не тронусь , Расскажи ещё про конус. -Воронка и есть в виде конуса лейка. Ну-ка, найди мне её поскорей-ка. Воронку я найти не смог, Но мама сделала кулёк, Картон вкруг пальца обкрутила И ловко скрепкой закрепила. Масло льётся, мама рада, Конус вышел то, что надо.
Cлайд 16
Объём конуса .
Cлайд 17
Удар! Удар! Ещё удар! Летит в ворота мячик - ШАР! А это- шар арбузный Зелёный, круглый, вкусный. Вглядитесь лучше - шар каков! Он сделан из одних кругов. Разрежьте на круги арбуз И их попробуйте на вкус.
Cлайд 18
Объём шара
Cлайд 19
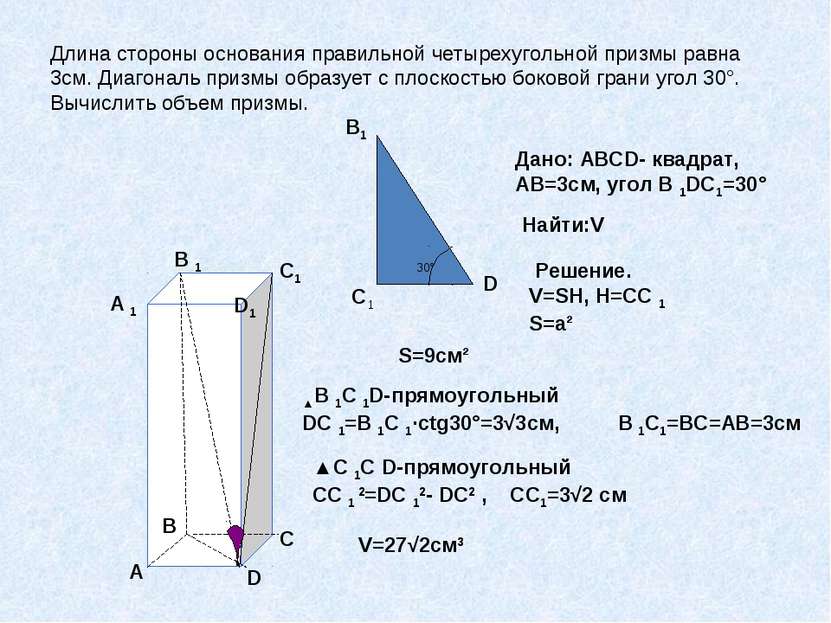
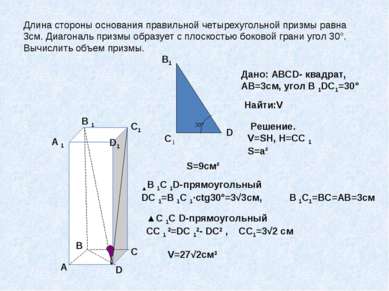Длина стороны основания правильной четырехугольной призмы равна 3см. Диагональ призмы образует с плоскостью боковой грани угол 30°. Вычислить объем призмы. А В С D A 1 B 1 C1 D1 C1 B1 D 30° Дано: АВСD- квадрат, АВ=3см, угол В 1DC1=30° Найти:V Решение. V=SH, H=СС 1 S=a² S=9cм² ▲В 1С 1D-прямоугольный DC 1=B 1C 1∙ctg30°=3√3см, В 1С1=ВС=АВ=3см ▲С 1С D-прямоугольный СC 1 2=DC 12- DC2 , СС1=3√2 см V=27√2см3
Cлайд 20
Практическая задача. Надо найти объём воды проходящёй за день в водонапорной вышке такого типа:
Cлайд 21
Решение. Во-первых это цилиндр. Объём цилиндра равен Сложность тут может доставить нахождение радиуса, но только с практической точки зрения. R=L/2π, где L-длина окружности, которую можно измерить верёвочкой. Установив все данные, подставим в формулу объёма. Но это ещё не всё, теперь умножаем объём на количество полных закачек за день, и мы получим полный объём воды проходящей через водонапорную башню.
Cлайд 22
Задачник. №1. Найдите объём правильной четырёхугольной пирамиды, если её диагональное сечение – равносторонний треугольник, площадь которого 12 √3 №2. В правильной четырёхугольной призме ABCDA’B’C’D’ высота в два раза длиннее стороны основания. Найдите объём призмы, если расстояние между серединами рёбер A’B’ и BC равно 3√2. №3. Через две образующие конуса, угол между которыми равен 30° проведено сечение, имеющее площадь 25 дм². найти объём конуса, если радиус основания 6 дм. №4. В конус вписан шар. Найти объём шара, если радиус основания конуса равен 3, а образующая равна 4. №5. Через точку А, лежащую на окружности основания цилиндра, проведена прямая, пересекающая окружность второго основания в точке В. Радиус цилиндра равен 5, длина отрезка АВ равна 4√5, расстояние между осью цилиндра и прямой АВ равно 3. найти объём цилиндра.
Cлайд 23
Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке где значения функции в соответствующих точках (на концах отрезка и в его середине). , и - Получила название в честь британского математика Томаса Симпсона (1710—1761).
Cлайд 24
http://mathprofi.ru/formula_simpsona_metod_trapecij.html http://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%A1%D0%B8%D0%BC%D0%BF%D1%81%D0%BE%D0%BD%D0%B0 Использованы ресурсы:
