X
Код презентации скопируйте его
Затухающие колебания
Скачать эту презентацию
Презентация на тему Затухающие колебания
Скачать эту презентациюCлайд 1
Лекция 26 Тема: Затухающие колебания 26.1. Свободные затухающие механические колебания; 26.2. Коэффициент затухания и логарифмический декремент затухания; 26.26. Свободные затухающие колебания в электрическом колебательном контуре; 26.27. Автоколебания; Сегодня: *
Cлайд 2
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается. Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например, маятник). Тогда сила трения (или сопротивления) , r - коэффициент сопротивления, - скорость движения. Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси Х max = - kx – r x, где kx - возвращающая сила, r x - сила трения. или md2x/dt2 = - kx - rdx/dt d2x/dt2 + (r/m)dx/dt + (k/m)x = 0.
Cлайд 3
Введем обозначения r/2m = k/m = 02 Тогда однородное дифференциальное уравнение второго порядка запишется d2x/dt2 + 2 dx/dt + 02x = 0 (26.1) Решение уравнения (26.1) имеет вид ( при 0 ) x = A0е- tcos( t +φ0) (26.2) A0 и 0 - определяются из краевых условий (начальных и граничных) задачи. и - из самого уравнения. - мы сами обозначили. Найдем . Здесь оно уже не равно 0 , т.е. 0 Подставим (26.2) в (26.1), но сначала найдем первую и вторую производные от (26.2): dx/dt = -A0βe- tcos( t + 0) - A0e - tsin ( t + 0); d2x/dt2 = 2A0e- tcos( t + 0) + A0e- tsin( t + 0) + + A0e - tsin( t + 0 ) - 2A0e - tcos ( t + 0 ).
Cлайд 4
Подставим эти значения в (26.1) и сократим на A0е- t 2cos( t + 0 ) + 2 sin( t + 0) - 2cos( t + 0) - 2 2cos( t + 0)- 2 sin( t + 0)+ 02cos( t + 0) = 0 Сократим на cos( t + 0 ) и выразим - 2 - 2 + 02 = 0 2 = 02- 2 = 02- 2 - круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение (26.1) будет только при 0 Для колебаний под действием различных сил (квазиупругих) значения , , 0 будут различными. Например, для колебаний под действием упругой силы 0 = k/m; = r/2m; = k/m - (r/2m)2. Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть - циклической (повторяющейся круговой) частотой можно лишь условно. По этой
Cлайд 5
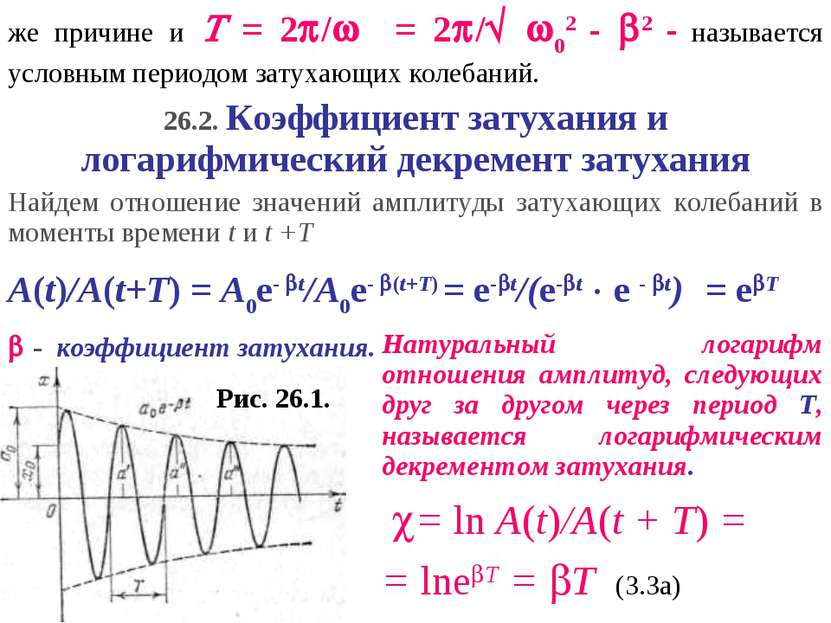
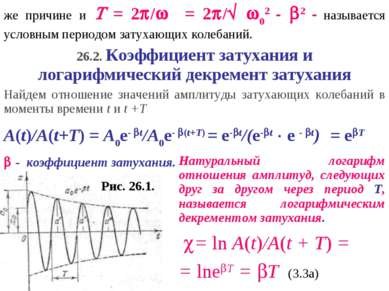Рис. 26.1. же причине и = 2 / = 2 / 02 - 2 - называется условным периодом затухающих колебаний. 26.2. Коэффициент затухания и логарифмический декремент затухания Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и t +T A(t)/A(t+T) = A0e- t/A0e- (t+T) = e- t/(e- t e - t) = e T - коэффициент затухания. Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания. = ln A(t)/A(t + T) = = lne T = T (З.За)
Cлайд 6
Выясним физический смысл и Обозначим через -время, в течение которого амплитуда А уменьшается в e раз. A0 /AΊ = e = e1, откуда β = 1, β = 1/ Следовательно, коэффициент затухания β - есть физическая величина, обратная времени, в течении которого амплитуда уменьшается в е раз. - время релаксации. Пусть Nе число колебаний, после которых амплитуда уменьшается в e раз, - время этих колебаний, тогда = ΝΤ, Τ= /Ν и = βΤ = / N = 1/N, = 1/N Следовательно, логарифмический декремент затухания есть физическая величина, обратная числу колебаний, по истечению которых амплитуда А уменьшается в e раз. Если = 0,01, то N = 100.
Cлайд 7
Для характеристики колебательной системы часто употребляется также величина θ = / = Ne, (З.Зб) Называемая добротностью колебательной системы. Как видно из её определения, добротность пропорциональна числу колебаний Ne, совершаемых системой за время , за которое амплитуда колебаний уменьшается в е раз. Подстановка функции (26.2) и её производной в выражение для полной энергии колеблющейся системы E = ½kx2 + ½m 2 приводит после преобразований к формуле (26.26)
Cлайд 8
Где = arctg( / ). График этой функции изображен на рис. 26.2. Рис. 26.2. Убывание энергии обусловлено работой силы сопротивления среды . Мощность, развиваемая этой силой, равна (–r )( )= –r 2. Т.о.,dE/dt = –r 2. Отсюда вытекает, что в тех точках кривой E(t) где = 0, касательная к кривой параллельна оси t. В остальных точках dE/dt < 0. При малом затухании (
Cлайд 9
остается постоянным. Продифференцировав выражение (26.27) по t, получим скорость возрастания энергии системы: dE/dt = - 2 tЕ0е-2 t = - 2 Е. Изменив знак на обратный, найдем скорость убывания энергии: -dE/dt = 2 Е. (26.5) Если энергия мало изменяется за время, равное периоду колебаний, убыль энергии за период можно найти, умножив выражение (26.5) на Т: - Е = 2 ТЕ (напомним, что Е обозначает приращение, а - Е – убыль энергии). Наконец, приняв во внимание формулы (26.26а) и (26.26б), придем к соотношению Е/(- Е ) = θ/2 , из которого следует, что при слабом затухании колебаний, добротность с точностью до множителя 2 равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний. Из формулы = 2 / 02 - 2 следует, что с ростом коэффициента затухания период колебаний увеличивается. При = 02 период колебаний обращается в бесконечность, т.е. движение
Cлайд 10
перестает быть периодическим. При > 0 корни характеристичес- кого уравнения становятся вещественными и решение дифферен- циального уравнения (26.1) оказывается равным сумме двух экспонент: х = С1е- 1t + С2е- 2t , где 1= - +i , а 2= - - i , а С1 и С2 - вещественные константы, значения которых зависят от нача- льных условий (от х0 и 0). Следовательно движение носит апериодический (непериодический) характер – выведенная из поло- жения равновесия система возвращается в положение равновесия, не совершая колебаний. На рис. 26.26 показано три возможных способа возвращения системы к положению равновесия при апериодическом движении. Каким из этих способов приходит Рис. 26.26. система в положение равновесия, зависит от начальных условий. Движение, изображаемое кривой В, получается в том случае, когда система начинает двигаться из положения, характеризуемого смещением х0, к положению равновесия с начальной скоростью 0, определяемым условием (26.6)
Cлайд 11
Это условие будет выполнено в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия. Если, отведя систему из положения равновесия, отпустить ее без толчка (т.е. с 0 = 0) или сообщить ей толчок недостаточной силы (такой, что 0 окажется меньше определяемой условием (26.6)), движение будет Происходить в соответствии с кривой А на рис. 26.26. 26.26. Свободные затухающие колебания в электрическом колебательном контуре Дифференциальное уравнение свободных затухающих колебаний заряда в контуре при (R 0) имеет вид (см. формулу1.6.2 в 1-й лекции) Используя формулу (1.6.27) 0 = 1/ LC и принимая коэффициент затухания
Cлайд 12
= R/2L (26.26.1) Дифференциальное уравнение можно записать следующим образом (26.26.2) Из выражений (26.1) и (26.2) вытекает, что колебания заряда совершаются по закону Q = Qmе- tcos( t + 0) (26.26.3) С частотой = 02- 2 = 1/LC – R2/27L2, (26.26.27) меньшей собственной частоты контура 0, а периодом больше, чем период собственных колебаний. При R = 0 формула (26.26.2) переходит в формулу (1.6.2а). Логарифмический декремент затухания определяется формулой = lnA(t)/A(t + T) = lne T = T, а добротность колебательного контура (26.26.5)
Cлайд 13
В заключение отметим, что при увеличении коэффициента затухания период затухающих колебаний растет и при = обращается в бесконечность, т.е. Движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически приближается к нулю, когда t . Процесс не будет колебательным. Он называется апериодическим. 26.27.Автоколебания При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту убыль энергии, колебания станут незатухающими. Пополнение энергии системы может осуществляться за счет толчков извне, однако эти толчки должны сообщаться системе в такт с ее колебаниями, в противном случае они могут ослабить колебания и даже прекратить их совсем. Можно сделать так, чтобы колеблющаяся система сама управляла внешним воздействием, обеспечивая согласованность сообщаемых ей толчков со своим движением. Такая система называется а в т о к о л е б а т е л ь н о и, а
Cлайд 14
Рис. 26.27. в качестве примера автоколебательной системы рассмотрим часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом — анкером (рис. 26.27). На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо упирается одним из зубьев в боковую поверхность той либо иной палетты, скользящей при качании маятника по поверхности зуба. Только в моменты, когда маятник находится вблизи
Cлайд 15
среднего положения, палетты перестают преграждать путь зубьям и ходовое колесо проворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качаний маятника (за период) ходовое колесо проворачивается на два зуба, причем каждая из палетт получает по толчку. Посредством этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения.
Cлайд 16
