X
Код презентации скопируйте его
Тригонометрические функции и их графики
Скачать эту презентацию
Презентация на тему Тригонометрические функции и их графики
Скачать эту презентациюCлайд 1
Cлайд 2
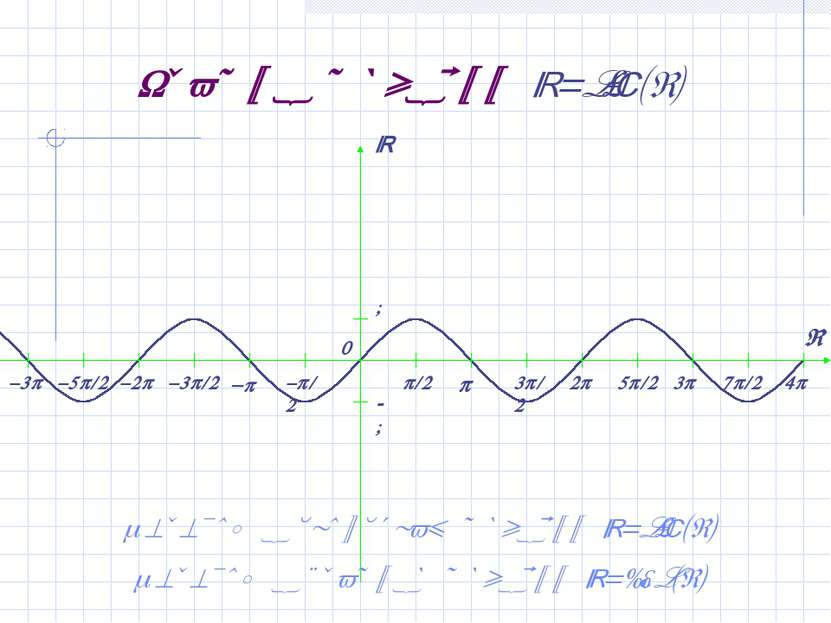
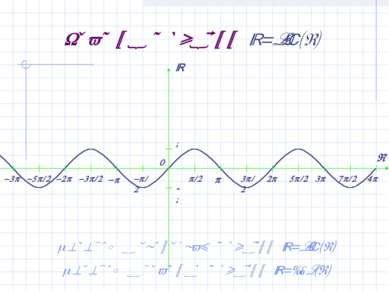График функции y=sin(x) Переход к свойствам функции y=sin(x) Переход к графику функции y=cos(x)
Cлайд 3
Свойства функции y=sin(x) Область определения y=sin(x) – множество R всех действительных чисел. Множество значений y=sin(x) – отрезок [-1;1]. Функция периодическая: sin(x)=sin(x+2pn) , n Z. Функция нечётная: sin(x)=-sin(-x). Функция принимает нулевые значения в точках, кратных p. Функция y=sin(x) принимает максимальное значение, равное 1, в точках x=p/2 + 2pn, n Z. Функция y=sin(x) принимает минимальное значение, равное -1 в точках x=-p/2 + 2pn , n Z. Между этими точками функция y=sin(x) монотонно убывает или монотонно возрастает. Вернись обратно к графику и найди на нём все указанные свойства функции y=sin(x) !
Cлайд 4
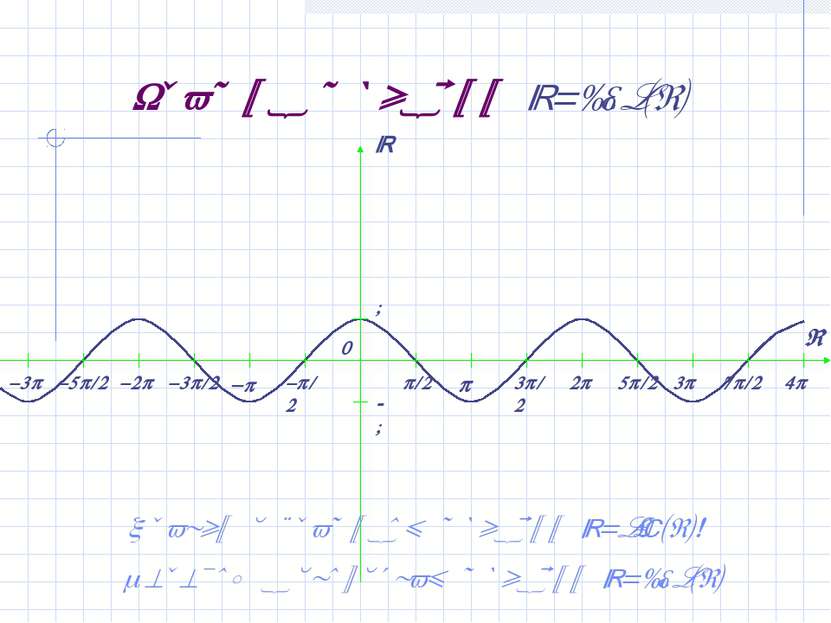
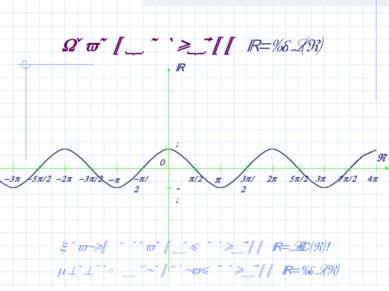График функции y=cos(x) Сравни с графиком функции y=sin(x)! Переход к свойствам функции y=cos(x)
Cлайд 5
Свойства функции y=cos(x) Область определения y=cos(x) – множество R всех действительных чисел. Множество значений y=cos(x) – отрезок [-1;1]. Функция периодическая: cos(x)=cos(x+2pn) , n Z. Функция чётная: cos(x)=cos(-x). Функция y=cos(x) принимает нулевые значения в точках x=p/2 + pn , n Z. Функция y=cos(x) принимает максимальное значение, равное 1, в точках x=2pn , n Z. Функция y=cos(x) принимает минимальное значение, равное -1 в точках x= (2n+1 ) p, n Z. Между этими точками функция y=cos(x) монотонно убывает или монотонно возрастает. Вернись обратно к графику и найди на нём все указанные свойства функции y=cos(x) !
Cлайд 6
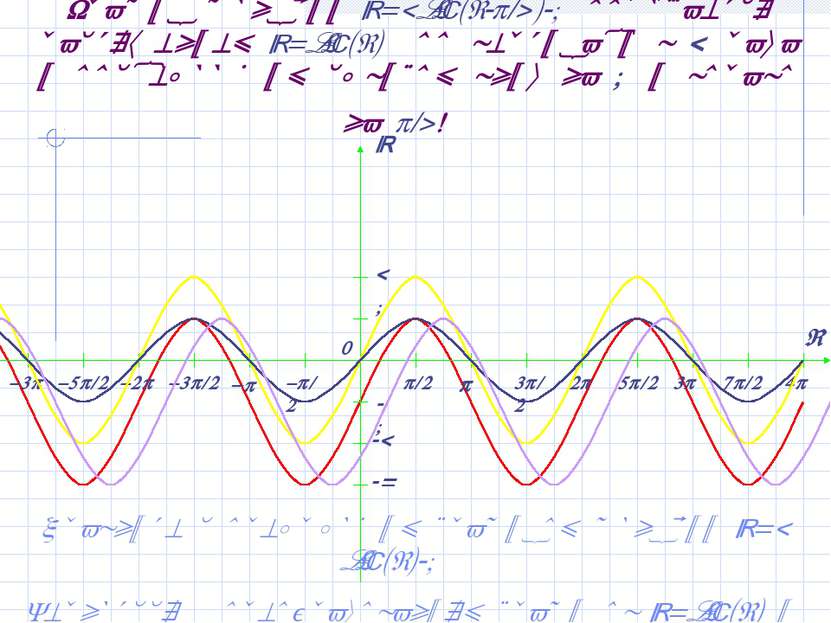
Преобразования графиков функций sin(x) и cos(x) y= -sin(x) y= sin(x- ) y= sin(x+ /2) y= sin(x- /4) y= sin(x)+2 y= 2sin(x)-1 y= 2sin(x- /4)-1 y= -cos(x) y= cos(x+ ) y= cos(x- /2) y= cos(x+ /4) y= cos(x)-1 y= 2cos(x)+1 y= 2cos(x+ /4)+1
Cлайд 7
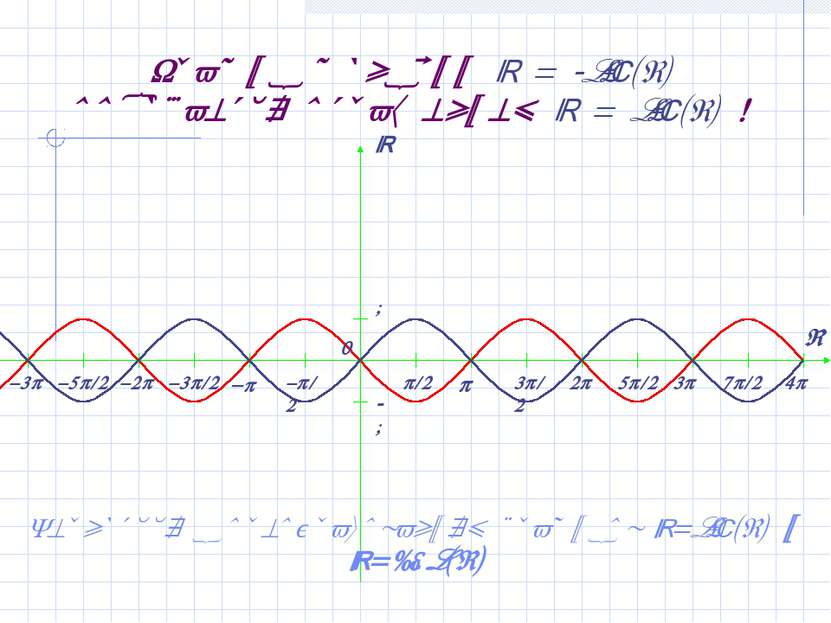
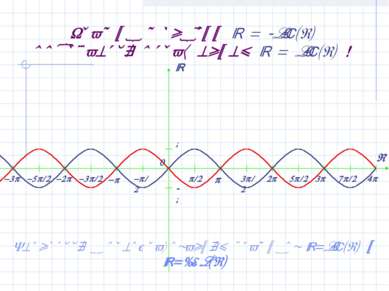График функции y = -sin(x) получается отражением y = sin(x) ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 8
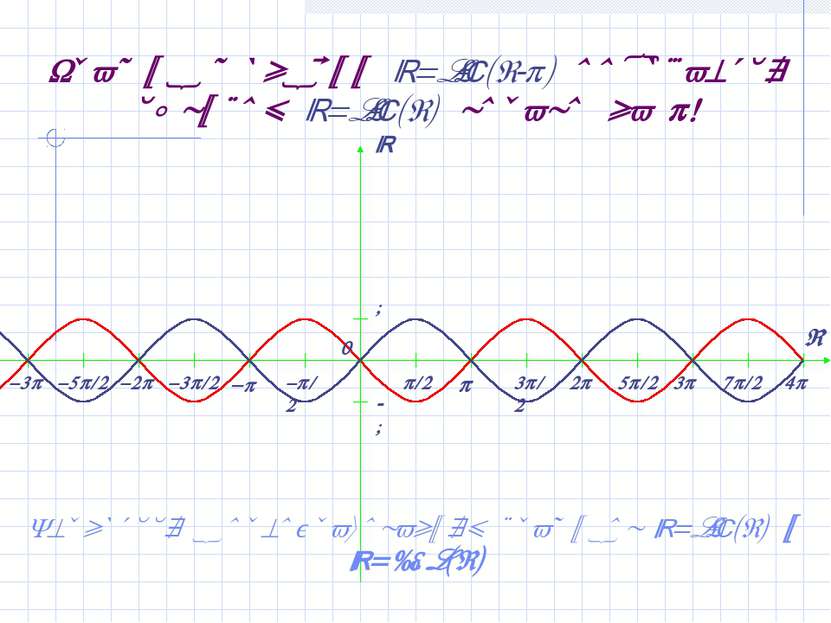
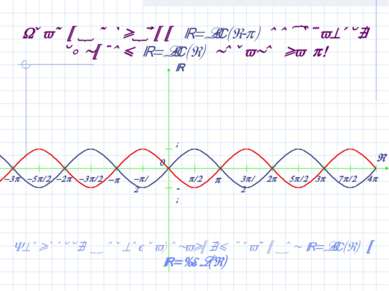График функции y=sin(x- ) получается сдвигом y=sin(x) вправо на ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 9
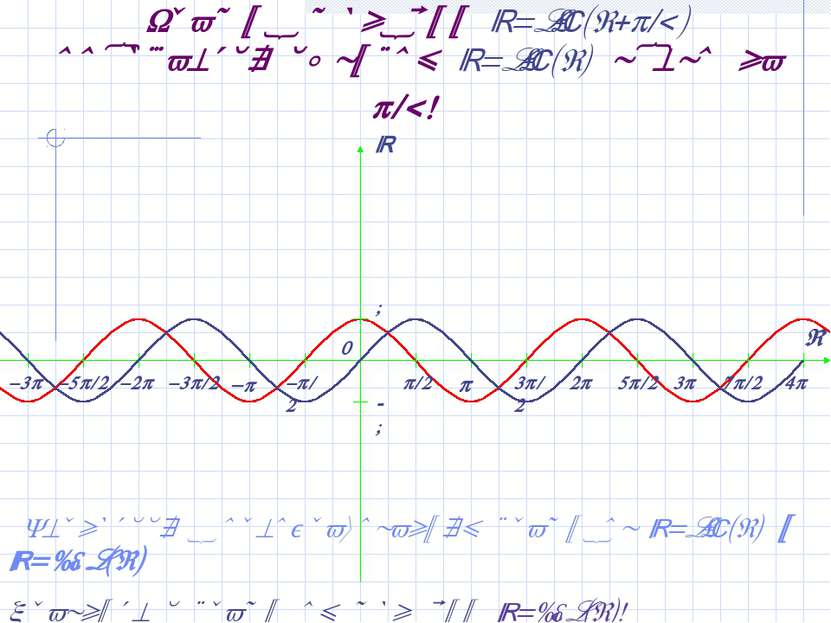
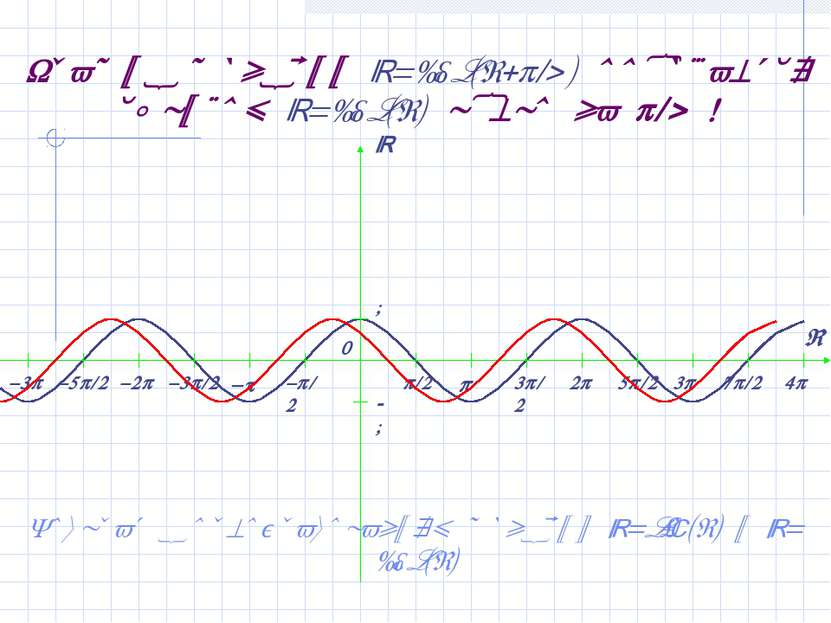
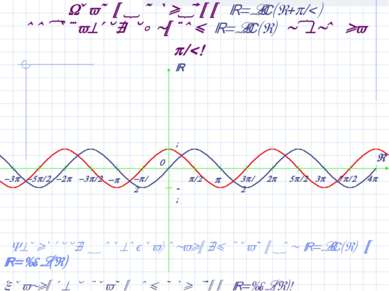График функции y=sin(x+ /2) получается сдвигом y=sin(x) влево на /2! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x) Сравните с графиком функции y=cos(x)!
Cлайд 10
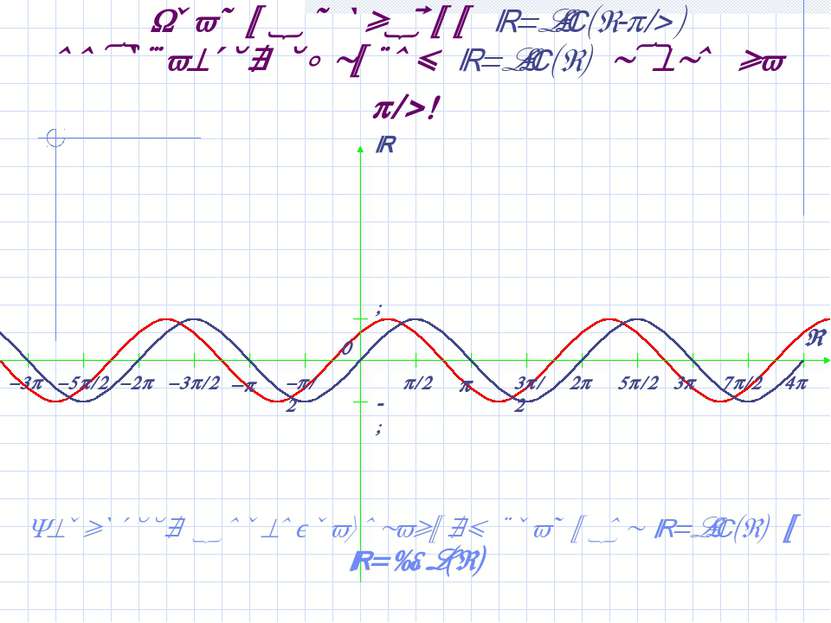
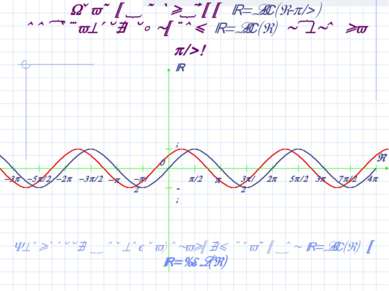График функции y=sin(x- /4) получается сдвигом y=sin(x) влево на /4! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 11
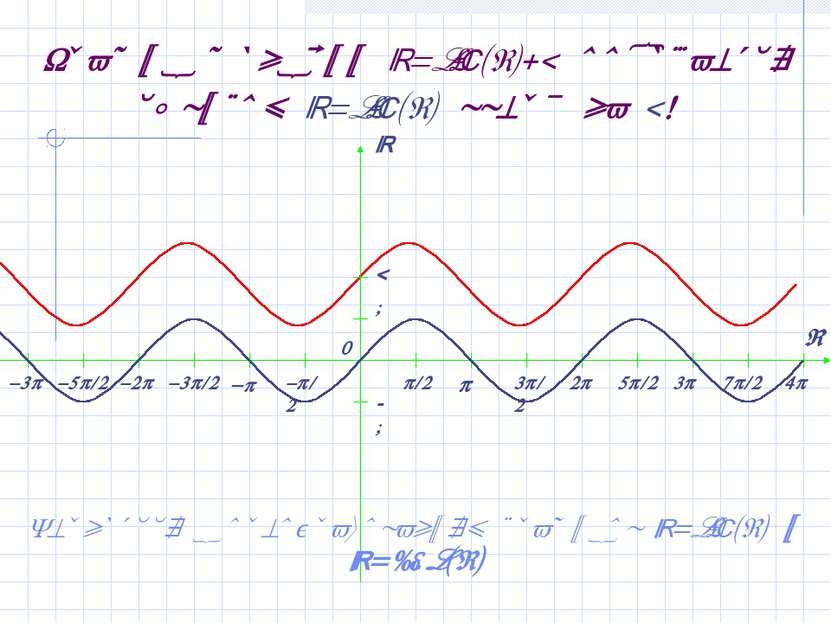
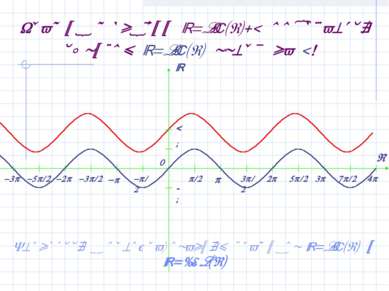График функции y=sin(x)+2 получается сдвигом y=sin(x) вверх на 2! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 12
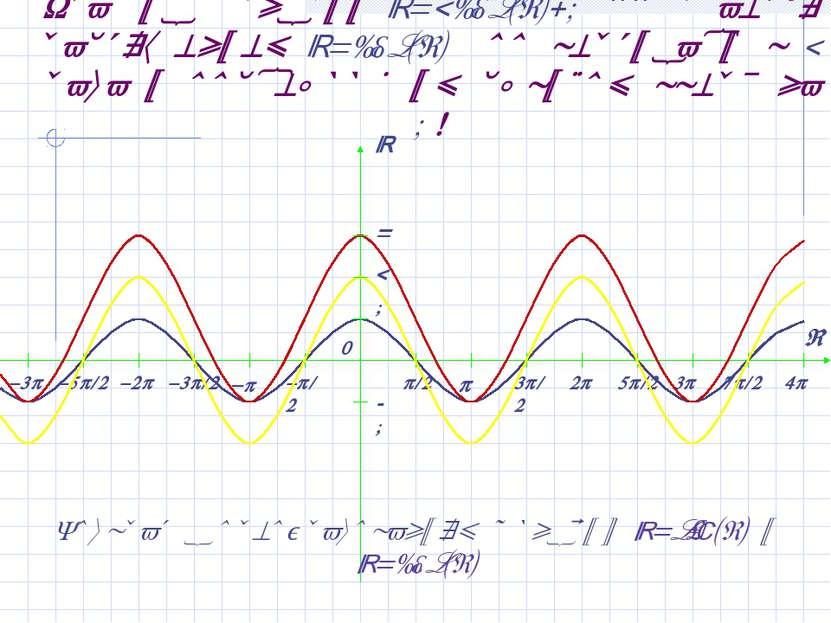
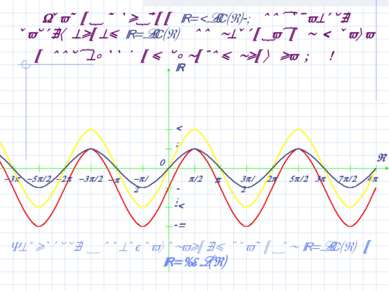График функции y=2sin(x)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 13
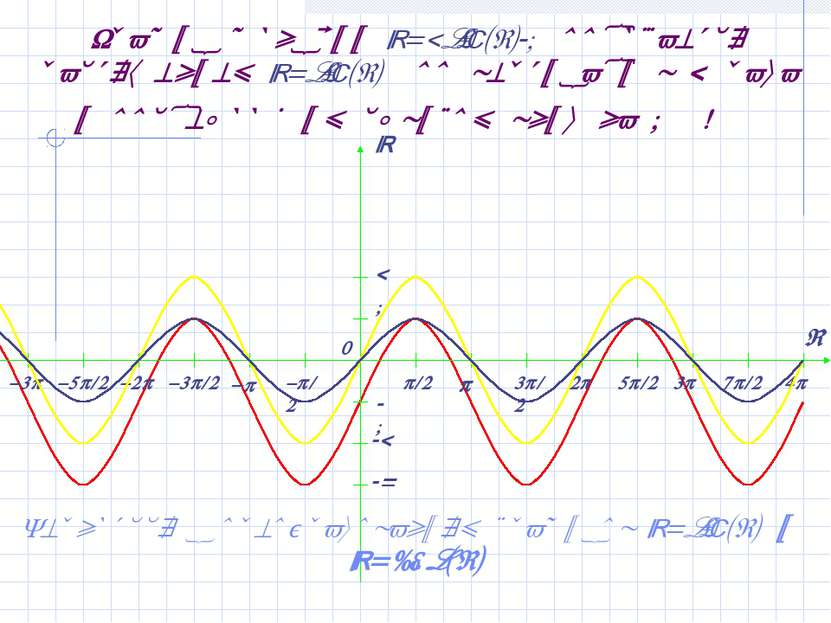
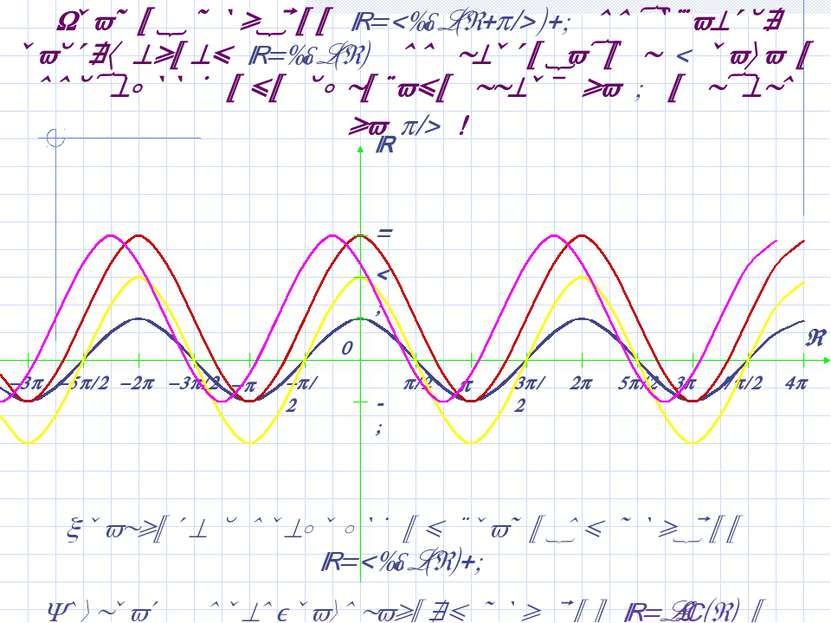
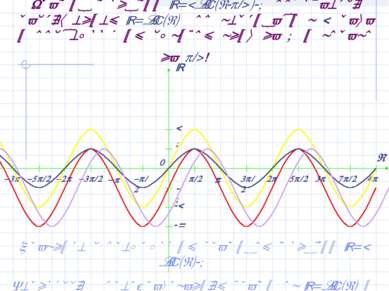График функции y=2sin(x- /4)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 и вправо на /4! Сравните с предыдущим графиком функции y=2sin(x)-1 Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)
Cлайд 14
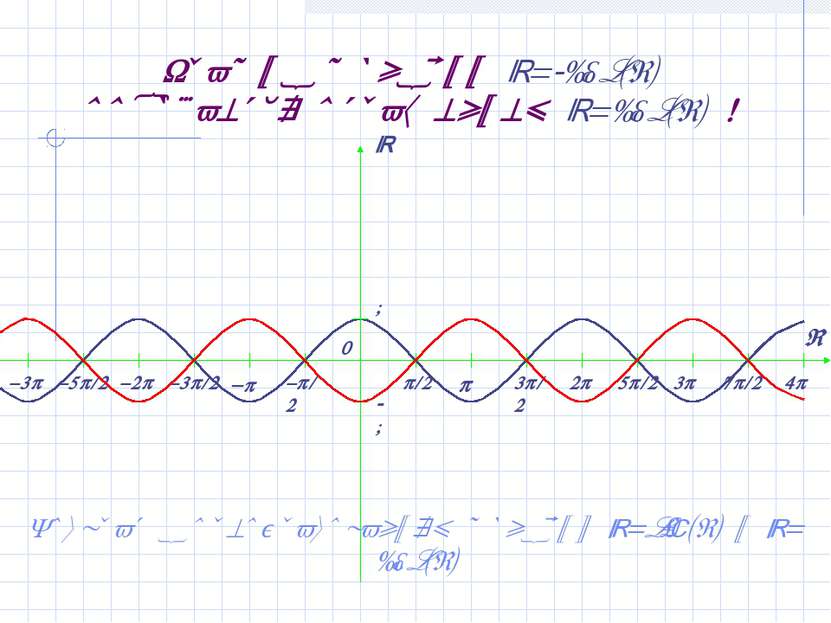
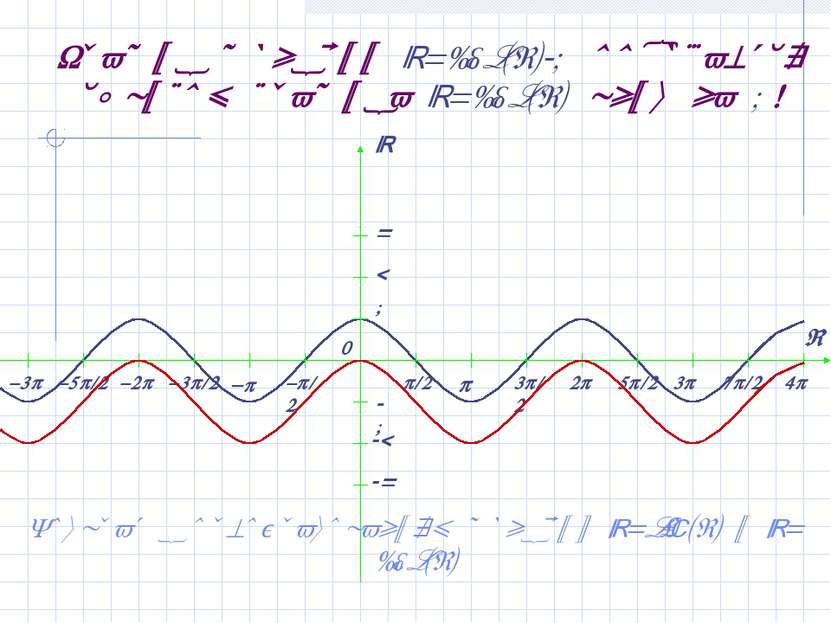
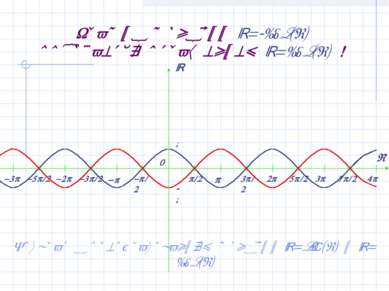График функции y=-cos(x) получается отражением y=cos(x) ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 15
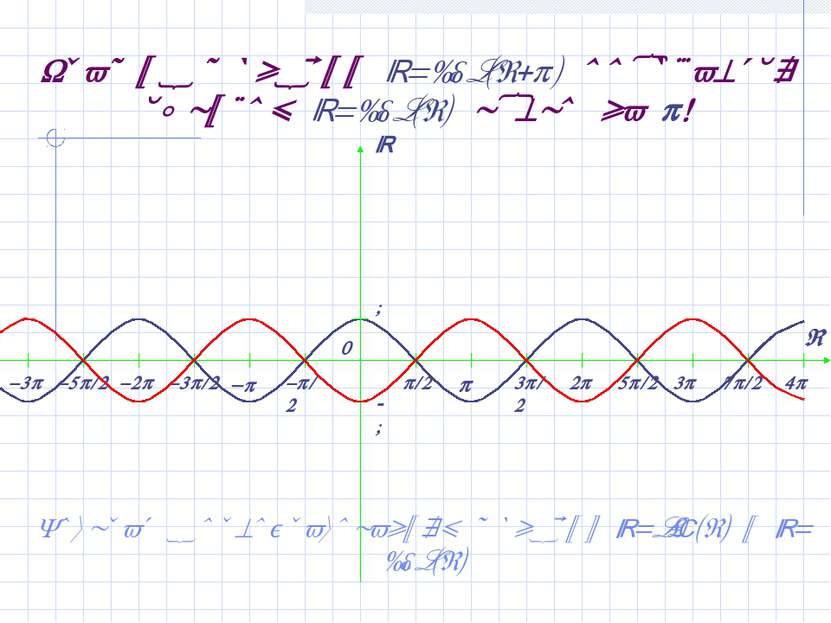
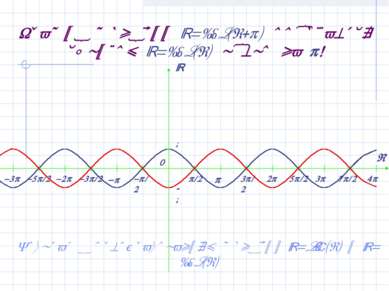График функции y=cos(x+ ) получается сдвигом y=cos(x) влево на ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 16
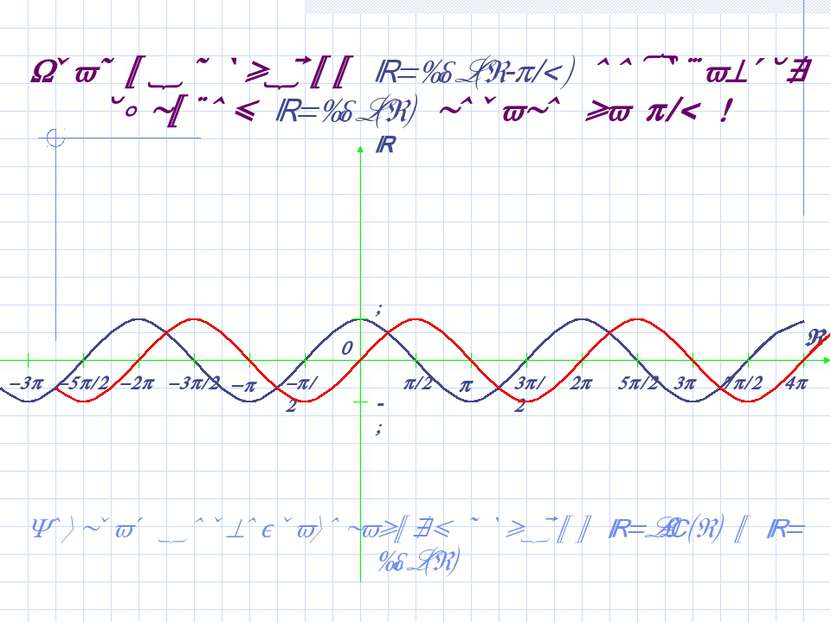
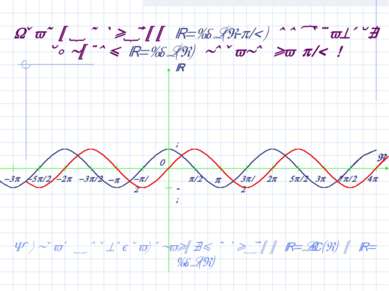График функции y=cos(x- /2) получается сдвигом y=cos(x) вправо на /2 ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 17
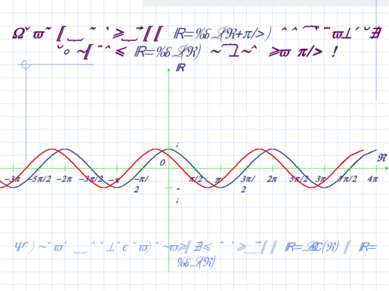График функции y=cos(x+ /4) получается сдвигом y=cos(x) влево на /4 ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 18
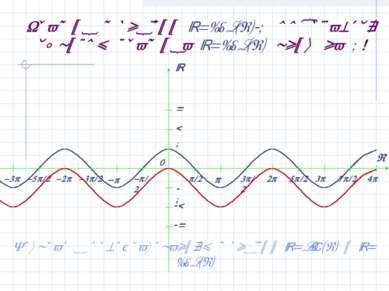График функции y=cos(x)-1 получается сдвигом графика y=cos(x) вниз на 1! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 19
График функции y=2cos(x)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующим сдвигом вверх на 1! Возврат к преобразованиям функций y=sin(x) и y=cos(x)
Cлайд 20
График функции y=2cos(x+ /4)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующими сдвигами вверх на 1 и влево на /4 ! Сравните с предыдущим графиком функции y=2cos(x)+1 Возврат к преобразованиям функций y=sin(x) и y=cos(x)
